Hipotesis kekontinuan

Pertanyaan berikutnya yang bisa diajukan: Di mana letak 𝔠 dalam daftar ℵ₀, ℵ₁, ℵ₂, dan seterusnya?

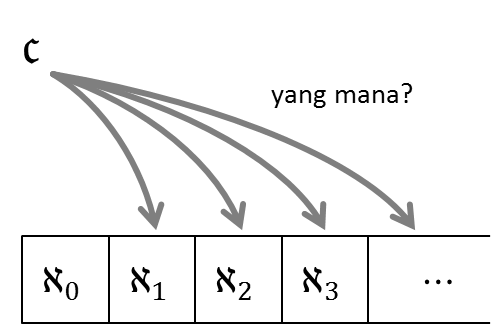
Sulit untuk mengetahuinya. Namun Cantor membuat sebuah hipotesis mengenai ini. Hipotesis berarti dugaan yang belum bisa dibuktikan. Ini disebut sebagai hipotesis kekontinuan (continuum hypothesis). Bunyinya adalah sebagai berikut:

Tidak ada himpunan yang kardinalitasnya berada di antara kardinalitas bilangan asli dan bilangan real.

Atau dalam simbol yang telah kita buat sebelumnya:

Tidak ada himpunan A yang kardinalitasnya berada di antara ℵ₀ dan 𝔠.

Atau dalam simbol matematika dituliskan:

\neg\exists A \in S:\aleph_{0} < | A |<\mathfrak{c}

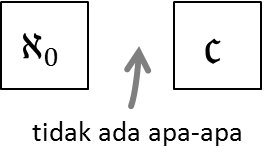
Hipotesis tersebut dapat dituliskan ulang dalam bentuk yang lebih sederhana, yaitu:

\aleph_{1}=\mathfrak{c}

Namun ini hanya hipotesis. Dalam sisa hidupnya Cantor berusaha membuktikan hipotesis kekontinuan ini. Pekerjaan ini sangat sulit.

Masih ingat dengan sistem MIU? Dalam sistem deduktif seringkali kita mencoba membuktikan suatu pernyataan berdasarkan aturan yang diberikan, tetapi tak kunjung menemukan jawaban. Bisa jadi pernyataan itu benar, bisa jadi salah, tetapi bisa jadi memang pernyataan itu tak dapat dibuktikan di dalam sistem yang kita miliki (undecidable).

Inilah yang dialami Cantor, ia tidak berhasil membuktikannya, sehingga pada akhir hidupnya ia masih belum tahu apakah hipotesis kekontinuan ini benar atau salah.

Ternyata memang undecidable

Pada tahun 1940, Kurt Gödel menunjukkan bahwa hipotesis kekontinuan tak dapat dibuktikan salah. Dilanjutkan tahun 1964 oleh Paul Cohen, beliau menunjukkan bahwa hipotesis kekontinuan ini tidak dapat dibuktikan benar. Artinya hipotesis kekontinuan adalah undecidable: bisa diasumsikan benar, bisa diasumsikan salah, tanpa mengakibatkan kontradiksi pada teori himpunan.

A Hierarchy of Infinities - PBS Infinite Series

How Big are All Infinities Combined? - PBS Infinite Series

Berikutnya: 1 dimensi dengan 2 dimensi