Kardinalitas, Aleph, dan fraktur c

Banyaknya anggota himpunan disebut sebagai kardinalitas.

Kardinalitas bilangan asli disimbolkan sebagai \aleph_{0} (aleph naught – alef nol). Alef adalah huruf A dalam bahasa Ibrani.

\left| \mathbb{N} \right| = \aleph_{0}

Kardinalitas bilangan real disimbolkan sebagai \mathfrak{c} (fraktur c).

\left| \mathbb{R} \right|\mathfrak{= c}

Sebelumnya juga telah kita buktikan bahwa kardinalitas himpunan bilangan asli, bilangan bulat, dan bilangan rasional adalah sama, sementara kardinalitas bilangan real dan interval-interval di dalamnya juga sama. Karena itu:

\left| \mathbb{N} \right| = \left| \mathbb{Z} \right| = \left| \mathbb{Q} \right| = \aleph_{0}

\left| \mathbb{R} \right| = \left| \left( 0,1 \right) \right| = \left| \left( 0,1 \right\rbrack \right|\mathfrak{= c}

Karena kardinalitas bilangan asli lebih sedikit dari bilangan real, berarti:

\left| \mathbb{N} \right| < \left| \mathbb{R} \right|

\aleph_{0}\mathfrak{< c}

Dengan adanya kardinalitas tak berhingga yang lebih tak berhingga dari tak berhingga lainnya, maka akan terdapat banyak tingkat kardinalitas tak berhingga yang lain. Pembuktiannya tidak dijelaskan di sini.

\aleph_{0} < \aleph_{1} < \aleph_{2} < \aleph_{3} < \ldots

Ini luar biasa sekali! Ternyata tak berhingga bukan hanya satu macam, tetapi berlapis-lapis. Ada langit di atas langit. Selalu ada kardinalitas yang lebih tinggi dari kardinalitas tak berhingga tingkat tertentu.

Kardinalitas ℵ₁ adalah kardinalitas tak berhingga pertama yang lebih tinggi dari ℵ₀. ℵ₂ adalah kardinalitas tak berhingga pertama yang lebih tinggi dari ℵ₁, dan seterusnya.

Bagaimana menulis huruf alef?

Alef adalah huruf pertama dalam bahasa Ibrani. Dalam bentuk cetak dituliskan sebagai:

ℵ

Kamu memerlukan tiga goresan untuk menuliskan huruf alef. Bayangkan tempat meuliskan huruf berbentuk kotak. Goresan pertama adalah diagonal dari pojok kiri atas ke pojok kanan bawah, goresan kedua dari ujung kanan atas ke tengah, dilanjutkan dengan goresan ketiga. Kamu dapat melihat urutannya secara lebih jelas pada gambar di bawah ini.

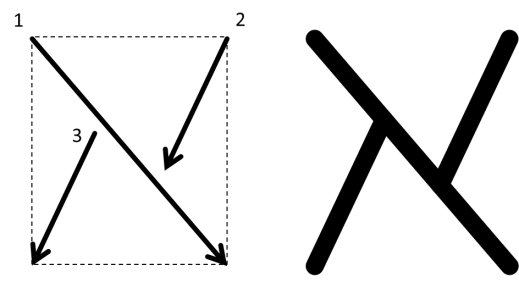
Apakah penggunaan simbol aleph ini merupakan wujud dari konspirasi para Zionis untuk menguasai dunia? Saya yakin tidak, karena peminjaman simbol dari budaya tertentu adalah hal yang biasa dalam matematika. Georg Cantor adalah orang Jerman, yang tentunya akan lebih terbiasa melihat tulisan Ibrani, Yunani, dan Latin daripada huruf Arab maupun Jawa.

Sebagai catatan tambahan mengenai hal ini, angka-angka yang kita gunakan diadopsi dari Arab. Bukan hanya angkanya saja, melainkan juga sistem penulisannya.

Alih-alih menuduh sesuatu sebagai konspirasi, belajarlah baik-baik agar suatu hari kamu menjadi matematikawan hebat yang memperkenalkan huruf nusantara. Bayangkan menggunakan huruf tradisional Sunda sebagai simbol matematika yang muncul dalam makalah-makalah matematika di seluruh dunia. Memang tidak perlu bangga karena penggunaan simbol baru seperti ini sangat biasa dalam dunia matematika, tetapi setidaknya hal ini bisa menjadi motivasi, bukan? Pada waktu itu kamu akan menemukan bahwa sebagian orang mengira ada konspirasi Sunda Empire di baliknya.

Berikutnya: Hipotesis kekontinuan