Interval (0, 1) dengan bilangan real

sejarah
pemikiran
tokoh

Interval (0, 1) adalah himpunan bagian dari keseluruhan bilangan real.

\left( 0,1 \right)\mathbb{\subset R}

Sekilas lagi… tampaknya interval tersebut akan mengandung lebih sedikit bilangan dibandingkan bilangan real secara keseluruhan. Namun lagi-lagi fungsi bijektif dapat dibuat. Misalnya fungsi berikut ini.

f\left( x \right) = \tan\left( \frac{1}{2}\pi\left( 2x - 1 \right) \right)

x \in \left( 0,1 \right)

Dalam diagram kartesius, grafiknya adalah seperti di bawah ini.

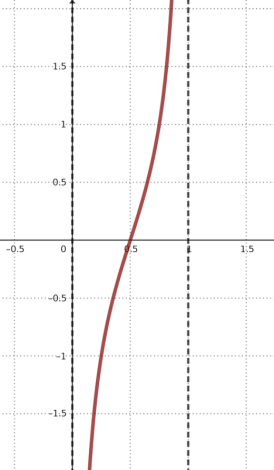
Terlihat bahwa dengan domain \left( 0,1 \right), fungsi tersebut memetakannya kepada range \left( - \infty, + \infty \right), yang adalah himpunan seluruh bilangan real.

Berikutnya: Interval (0, 1) dengan (0, 1]