Pembuktian Proposisi 32B
Jumlah sudut dalam sebuah segitiga sembarang sama besarnya dengan dua sudut siku-siku.
Pernyataan ini cukup jelas maksudnya, membicarakan tentang besar seluruh sudut gabungan dalam segitiga. Namun apakah pernyataan ini jelas kebenarannya? Sebagian orang mungkin percaya begitu saja, tetapi mereka sebenarnya berhak mempertanyakan kebenaran kalimat ini. Karena itu kita perlu membuktikannya.
Mari kita coba buktikan. Di bawah ini adalah segitiga sembarang dengan titik-titik sudut bernama A, B, dan C.

Tujuan kita adalah membuktikan bahwa sudut-sudut segitiga tersebut, yaitu α, β, dan γ, jika dijumlahkan akan bernilai sama dengan dua kali sudut siku-siku, atau 180°.

Pertama-tama, menurut postulat kedua, sebuah garis dapat diperpanjang sepanjang-panjangnya. Berarti ruas garis AB dapat diperpanjang ke arah kanan sepanjang-panjangnya.

Setelah itu, menurut postulat kelima, jika ada sebuah garis dan sebuah titik di luar garis itu, dapat dibuat satu dan hanya satu garis lain yang melalui titik tersebut dan sejajar garis pertama.
Dalam gambar terdapat garis AC dan titik B yang letaknya di luar AC. Berarti kita dapat membuat garis lain yang melalui titik B dan sekaligus sejajar dengan AC. Sebut saja garis itu g. Gambarnya adalah seperti di bawah ini. Tidak ada kemungkinan lain, karena postulat kelima menjamin bahwa garis yang dapat dibuat hanya ada satu macam.
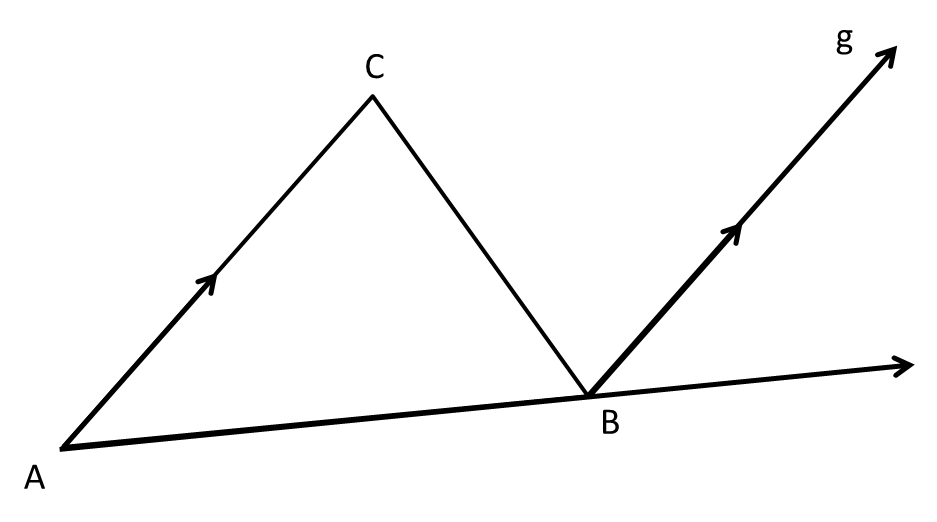
Mari kita pasang label sudutnya.

Terlihat bahwa sudut α, β, dan γ membentuk sebuah garis lurus, yang besarnya tentu saja 180°.

Dengan demikian kita telah berhasil membuktikan bahwa
Pranala mengenai Euclid
Beberapa artikel dan video mengenai Euclid dapat kamu baca atau tonton melalui:
- EUCLID OF ALEXANDRIA – The Father of Geometry
- Mathigon: Euclidean Geometry
- Euclid's Geometry
- The 5 Postulates of Euclid
- Euclid's first four postulates
Berikutnya: Pengaruh Euclid dalam dunia non-matematika