Sudut segitiga lebih dari 180°

Masih ingat dengan pembuktian proposisi 32b geometri Euclid? Di sana telah dibuktikan bahwa jumlah sudut dalam segitiga adalah 180°.

Perhatikan bahwa pembuktian tersebut bergantung pada postulat 5 untuk membentuk garis sejajar AC yang melalui titik B. Karena postulat 5 diganti dalam geometri eliptik, maka pembuktiannya juga akan berubah. Singkat cerita, dalam geometri eliptik, jumlah sudut dalam segitiga akan lebih dari 180°. Contohnya adalah segitiga berikut ini.

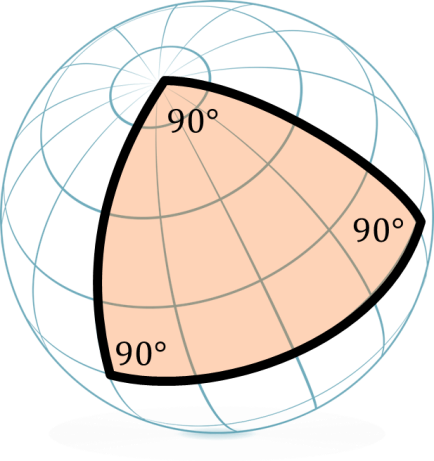
Bayangkan kamu bergerak dari ekuator ke kutub utara. Kemudian kamu menghadap kanan, lalu meneruskan perjalanan hingga sampai ke ekuator, menghadap kanan lagi, berjalan lagi, hingga kembali ke titik semula. Di titik semula itu, kamu menghadap kanan kembali untuk menghadap utara. Karena yang kamu lakukan adalah menghadap kanan, berarti sudut-sudut yang kamu buat semuanya adalah 90°, yang berarti segitiga itu memiliki jumlah sudut 270°. Sesuatu yang tidak mungkin terjadi pada bidang datar.

Ternyata, pemahaman manusia tentang geometri sepanjang sejarah hingga abad ke-18 bukanlah satu-satunya geometri. Geometri Euclid ternyata hanya berlaku pada bidang atau ruang datar. Karena sejak lahir manusia dibiasakan untuk membayangkan bidang dan ruang secara demikian, manusia merasa bahwa ini adalah satu-satunya geometri, satu-satunya kebenaran mengenai ruang tempat kita tinggal.

Geometri sferikal jelas tidak membantu kita secara langsung dalam kehidupan sehari-hari, karena kita berurusan dengan jalanan, gedung, meja yang datar. Dalam skala kecil, geometri Euclid jelas lebih praktis. Kelengkungan bumi tidak terlalu penting untuk diperhitungkan ketika kita hendak pergi dalam jarak 1 km (itulah sebabnya ada orang yang mati-matian membela kepercayaan bahwa bumi datar). Namun perjalanan menggunakan pesawat terbang dan GPS sangat memerlukan hal ini, karena dalam skala sebesar itu, kelengkungan bumi menjadi sangat penting.

Berikutnya: Geometri Hiperbolik