Kecurigaan terhadap postulat 5
Telah dibahas sebelumnya bahwa geometri Euclid memberikan kepastian. Kepastian bahwa selama kita setuju dengan asumsi dasarnya, konsekuensinya sudah tertentu.
Namun bagaimana jika kita tidak setuju dengan asumsi dasar?
Beberapa ahli matematika mencurigai postulat kelima, karena tidak tampak jelas. Perhatikan keempat postulat pertama.
Ruas garis lurus dapat dibentuk dari satu titik ke titik yang lain.
Ruas garis dapat diperpanjang sepanjang-panjangnya.
Lingkaran dapat dibentuk menggunakan ruas garis sebagai jari-jari, dan salah satu titik ujungnya sebagai pusat lingkaran.
Semua sudut siku-siku adalah kongruen.
Dan kemudian postulat kelima:
Jika sebuah garis melalui dua garis lain, dan jumlah sudut dalam kedua garis tersebut pada sisi yang sama adalah kurang dari dua kali sudut siku-siku, maka kedua garis tersebut akan bertemu jika diperpanjang.

Postulat kelima tampak sangat rumit dan tidak begitu jelas dibandingkan postulat-postulat sebelumnya.
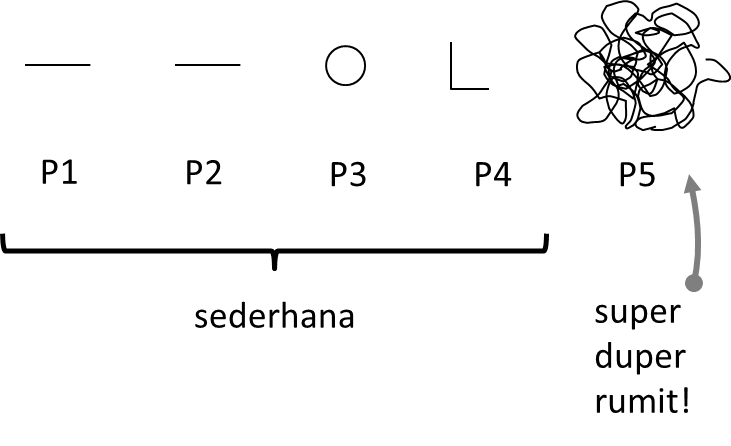
Ini membuat matematikawan-matematikawan sepanjang sejarah curiga. Jangan-jangan, postulat ini sebenarnya merupakan akibat dari postulat-postulat sebelumnya, atau dengan kata lain, postulat kelima ini bukan postulat tetapi proposisi.
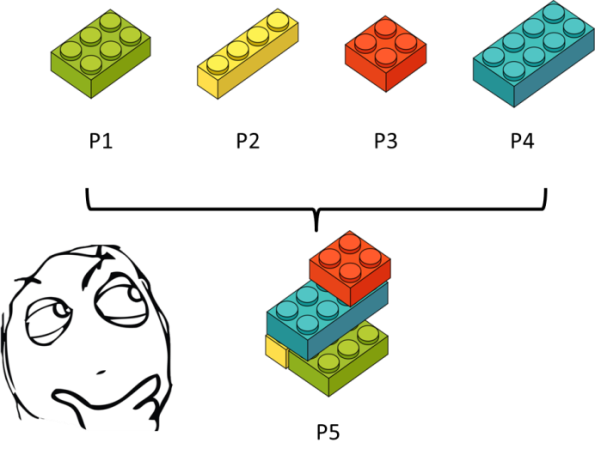
Sejumlah matematikawan yang berusaha membuktikan bahwa P5 bisa diturunkan dari postulat yang lain di antaranya adalah Ibn al-Haytham (abad 11), Omar Khayam (abad 12), Giovanni Girolamo Saccheri (abad 18), János Bolyai dan Nikolai Ivanovich Lobachevsky (abad 19). Hasilnya: Mereka gagal.
Walaupun pada abad 18 John Playfair mengubahnya menjadi kalimat yang lebih sederhana (yang artinya sama, tentu saja), tetap kesulitan ini tak dapat diatasi.
(Playfair) Diberikan sebuah garis dan sebuah titik di luar garis itu, terdapat tepat satu garis yang melalui titik tersebut yang sejajar garis yang semula.
Tidak satupun ahli matematika berhasil membuktikan bahwa P5 dapat diturunkan dari postulat lainnya. Ini tidak tentu berarti bahwa P5 tidak dapat dibuktikan dari yang lain. Ini hanya berarti bahwa P5 belum berhasil dibuktikan. Siapa yang tahu bahwa suatu saat akan ada yang berhasil membuktikannya?
Ingat bahwa ketika kita tidak berhasil membuktikan sebuah pernyataan dalam sistem, tidak tentu pernyataan tersebut undecidable. Mungkin saja demikian, tetapi mungkin saja kita kurang berusaha.
Namun ingat juga bahwa pernyataan yang undecidable dapat dibuktikan dari luar sistem. Artinya kita bertindak sebagai Tuhan di luar sistem dan mengutak-atik sistem dari luar. Inilah yang dilakukan oleh Carl Friedrich Gauss, Janos Bolyai, dan Nikolai Ivanovich Lobachevsky di abad 18. Mereka keluar dari sistem dan bertindak sedikit keterlaluan: Mencoba mengganti postulat 5 dengan yang lain, dan melihat akibat yang dapat muncul. Geometri yang dihasilkan ternyata konsisten dan ada dalam realitas. Geometri-geometri semacam ini disebut sebagai geometri non-Euclidean.
Contoh geometri non-Euclidean adalah geometri eliptik dan geometri hiperbolik.
Berikutnya: Geometri Eliptik