Geometri Eliptik
Geometri non-Euclidean yang pertama adalah geometri eliptik. Geometri eliptik memiliki 5 postulat juga.
Ruas garis lurus dapat dibentuk dari satu titik ke titik yang lain.
Ruas garis dapat diperpanjang sepanjang-panjangnya.
Lingkaran dapat dibentuk menggunakan ruas garis sebagai jari-jari, dan salah satu titik ujungnya sebagai pusat lingkaran.
Semua sudut siku-siku adalah kongruen.
Diberikan sebuah garis dan sebuah titik di luar garis itu, tidak ada garis yang melalui titik tersebut yang sejajar garis yang semula.
Keempat postulat pertama sama persis dengan geometri Euclid. Perbedaan hanya terdapat pada postulat kelima. Bandingkan postulat kelima geometri eliptik dengan geometri Euclid:
| Euclid | Eliptik |
|---|---|
| Diberikan sebuah garis dan sebuah titik di luar garis itu, terdapat tepat satu garis yang melalui titik tersebut yang sejajar garis yang semula. | Diberikan sebuah garis dan sebuah titik di luar garis itu, tidak ada garis yang melalui titik tersebut yang sejajar garis yang semula. |
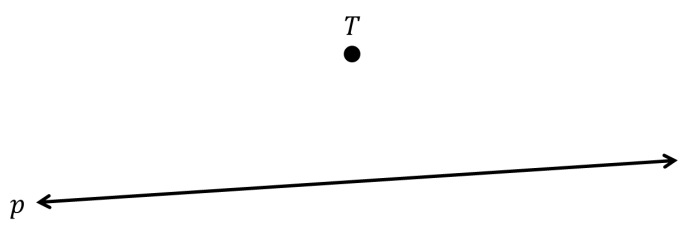
Akal sehat kita mengatakan bahwa kita akan selalu dapat membuat garis sejajar p yang melalui titik T. Selalu! Sekalipun kamu berpura-pura tidak dapat, hati nuranimu akan berteriak kencang, Aku melihatnya dengan jelas! Ini dapat dilakukan!
Lalu apakah geometri eliptik ini salah?
Geometri Euclid mengasumsikan bahwa bidang tempat kamu menggambar garis selalu datar. Kamu biasanya menggambar di atas kertas yang diletakkan di atas meja yang datar. Guru menulis di atas papan tulis yang datar. Geometri Euclid berlaku untuk bidang datar yang dapat diperluas menjadi ruang 3 dimensi yang memiliki sifat sama.
Karena hal inilah, manusia menerima begitu saja kebenaran geometri Euclid. Geometri Euclid begitu cocok dengan kebiasaan kita! Namun suatu teori yang cocok dengan kebiasaan kita tidak harus berarti cocok dengan segala keadaan di dalam alam semesta yang luas ini. Contohnya permukaan bumi.
Bumi itu bulat. Setidaknya menurut saya demikian. Definisi garis lurus pada permukaan bola sedikit berbeda dari definisi garis lurus pada bidang datar. Pada permukaan bulat seperti bola, ketika kita bergerak lurus, lintasan yang terjadi adalah melengkung mengikuti lengkungan permukaan bola.
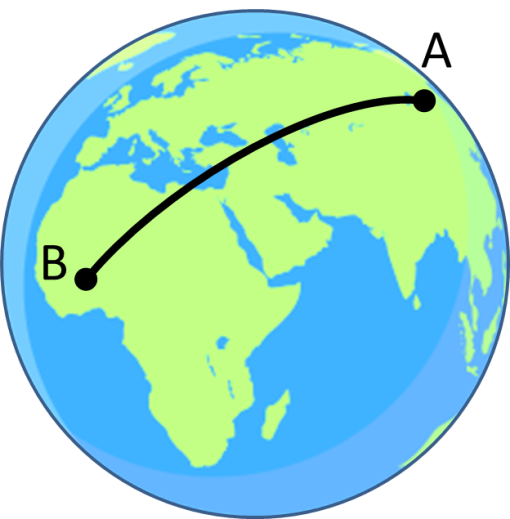
Jika kamu bergerak lurus terus di permukaan bumi, suatu saat kamu akan kembali ke posisimu yang semula. Berarti ruas garis lurus di permukaan bola yang diteruskan tanpa batas akan membentuk lingkaran yang jari-jarinya sama dengan jari-jari bola. Ini adalah jari-jari terbesar lingkaran yang dapat dibuat di permukaan bola.

Geometri sferikal adalah geometri pada permukaan bola. Setiap garis lurus yang dibuat pada permukaan bola akan membentuk lingkaran yang jari-jarinya sebesar jari-jari bola.
See the Pen Spherical by Ari Prasetyo (@ariprasetyo) on CodePen.
Dengan demikian tidak ada garis sejajar yang dibuat di permukaan bola, karena semua garis lurus yang kamu buat akan berpotongan satu sama lain. Ini seperti yang dinyatakan oleh postulat kelima geometri eliptik.
Diberikan sebuah garis dan sebuah titik di luar garis itu, tidak ada garis lurus yang melalui titik tersebut yang sejajar garis yang semula.
Geometri eliptik tidak harus terjadi di permukaan bola, tetapi yang terdapat di permukaan bola seperti ini memiliki nama khusus, yaitu geometri sferikal.

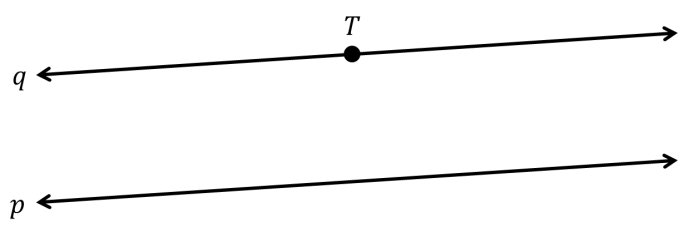
Mungkin kamu akan berpikir: Bagaimana dengan gambar berikut ini? Bukankah p dan q sejajar?

Dalam gambar di atas, jari-jari lingkaran q tidak sebesar jari-jari bola. Jika kamu menjalani lintasan tersebut, orang-orang di sekitarmu akan melihat bahwa lintasan yang kamu jalani tidaklah lurus, melainkan berbelok. Jadi garis q tidak cocok dengan definisi garis lurus di permukaan bola.
Geometri eliptik ini menghasilkan sejumlah konsekuensi yang tidak muncul dalam geometri Euclid.
Berikutnya: Ada bangun segidua