Bilangan asli dan bilangan bulat

Bilangan bulat (ℤ) memiliki anggota negatif, nol, maupun positif. Bilangan asli dimulai dari nol. Sekilas tampak bahwa bilangan bulat akan lebih banyak dari bilangan asli, karena terdapat tak berhingga bilangan bulat di sebelah kiri yang tidak memiliki pasangan bilangan asli.

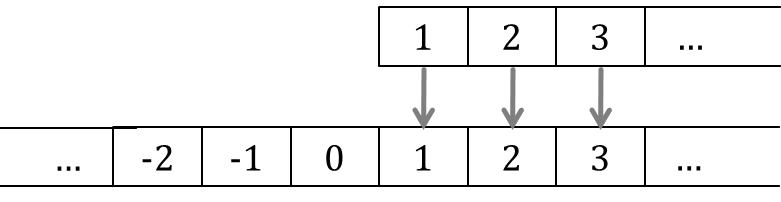
Berdasarkan prinsip sebelumnya, dua himpunan akan memiliki banyak anggota yang tepat sama jika fungsi bijektif dari himpunan pertama ke himpunan kedua dapat dibuat.

Fungsi bijektif seperti apa yang dapat kita buat untuk memetakan bilangan asli kepada bilangan bulat? Strateginya sederhana. Kita akan memisahkan bilangan asli bulat dan bilangan asli ganjil.

Bilangan asli ganjil akan kita petakan ke bilangan 0 dan bilangan negatif.

1	3	5	7	9	11	...
↓	↓	↓	↓	↓	↓
0	-1	-2	-3	-4	-5	...

Bilangan genap akan kita petakan pada bilangan bulat positif.

2	4	6	8	10	12	...
↓	↓	↓	↓	↓	↓
1	2	3	4	5	6	...

Keduanya adalah fungsi bijektif. Dengan menggabungkan keduanya secara berselang-seling, kita akan memperoleh fungsi bijektif yang memetakan bilangan asli kepada bilangan bulat.

y = \begin{cases} \frac{x}{2} &\text{jika } x \text{ genap} \\ \frac{1-x}{2} &\text{jika } x \text{ ganjil} \end{cases}

1	2	3	4	5	6	...
↓	↓	↓	↓	↓	↓
0	1	-1	2	-2	3	...

Alternatif lain

Fungsi bijektif lain juga dapat dibuat. Kamu dapat mengujinya sendiri bahwa jika fungsi di bawah ini diberi input bilangan asli akan menghasilkan bilangan bulat.

f\left( x \right) = \frac{1}{4}\left( \left( 2x - 1 \right)\left( - 1 \right)^{x} + 1 \right)

x\mathbb{\in N}

Berikutnya: Prinsip penomoran