Mesin penambah ekor 0
Sebagai contoh, mesin Turing berikut ini akan menambahkan simbol 0 di akhir rangkaian simbol yang terdiri dari 1 dan 0. Pita bertuliskan 111 akan menjadi bertuliskan 1110, 1101 akan menjadi 11010, dan seterusnya.
Mesin ini memiliki dua status, yaitu PROSES dan SELESAI.
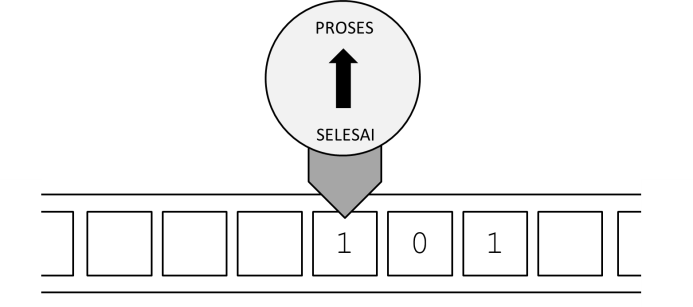
Ketika mulai, mesin Turing ini diatur sedemikian rupa sehingga status awalnya adalah PROSES, pita bertuliskan 101, dan head menunjuk simbol pertama dari 101.
Instruksi yang diberikan pada mesin Turing ini adalah sebagai berikut:
| State | Simbol terbaca | Instruksi | |
|---|---|---|---|
| 1 | PROSES | 0 |
Biarkan simbolnya, Maju, Status tetap PROSES. |
| 2 | PROSES | 1 |
Biarkan simbolnya, Maju, Status tetap PROSES. |
| 1 | PROSES | kosong |
Tulis 0, Maju, Status menjadi SELESAI. |
Berikut ini adalah yang akan terjadi ketika program dijalankan.
Mesin Turing berada pada status PROSES, head berada pada simbol pertama 101.
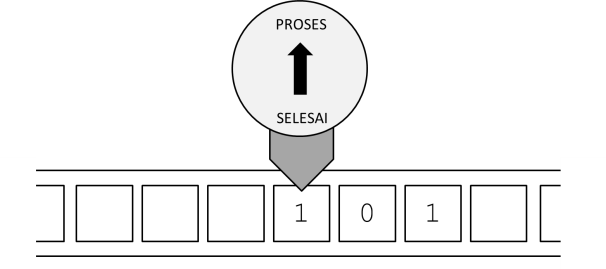
Karena kondisinya pada state PROSES dan simbol terbaca adalah 1, maka mesin akan menjalankan instruksi nomor 2, yaitu biarkan (yang sama sekali tidak mengubah simbol), maju ke sel berikutnya, dan menset status menjadi PROSES, yang artinya tidak mengubah status sama sekali.
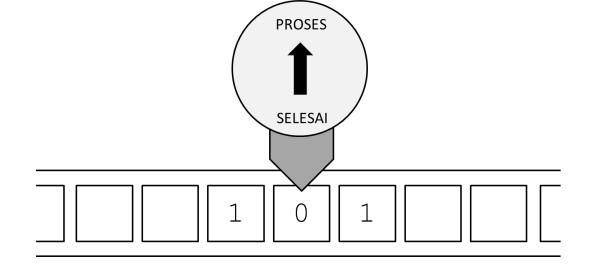
Berikutnya, karena kondisi mesin berada pada status PROSES dan simbol terbaca adalah 0, maka mesin akan melakukan instruksi nomor 1: Biarkan simbolnya, maju ke sel berikutnya, dan menset status menjadi PROSES lagi.
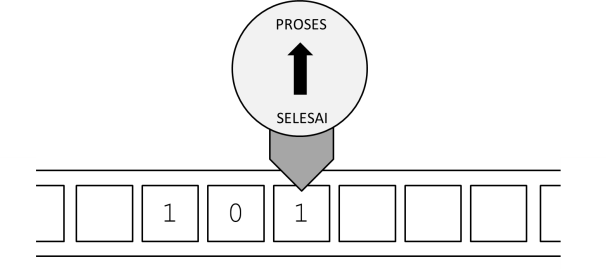
Berikutnya, kondisi mesin berada pada status PROSES dan simbol terbaca adalah 1, maka mesin kembali melakukan instrutksi nomor 2: Biarkan simbolnya, maju ke sel berikutnya, dan menset status menjadi PROSES lagi.
Sampai di sini, keadaan mesin adalah seperti pada gambar di bawah ini.
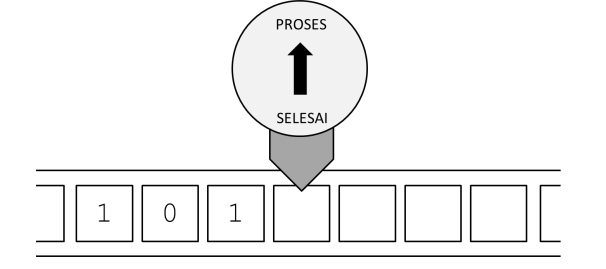
Karena mesin ini berada pada status PROSES dan simbol terbaca adalah kosong, maka sekarang instruksi 3 yang dilakukan, yaitu tulis simbol 0, ...
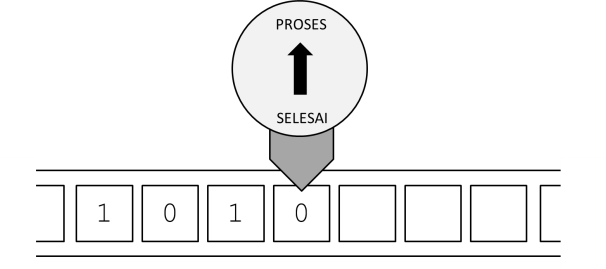
... maju ke sel berikutnya ...
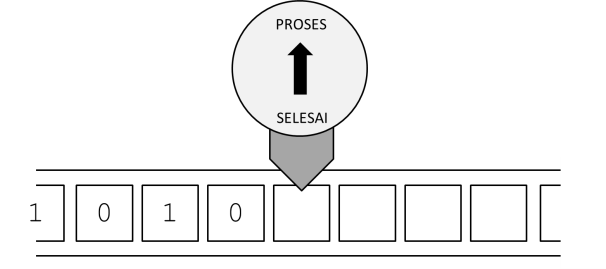
... dan kemudian mengganti status menjadi SELESAI.
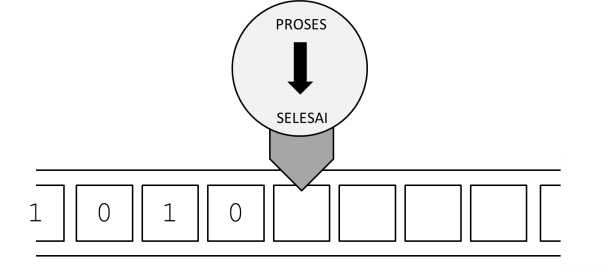
Sampai di sini, komputasi telah diselesaikan dengan status SELESAI, dan pada pita tertulis 1010. Dengan demikian, mesin Turing ini telah berhasil menambahkan ekor 0 pada 101 sehingga menjadi 1010.

Kamu dapat melihat kerja mesin ini dalam media interaktif berikut:
Mesin penambah ekor 0 - Mesin Turing ini diprogram untuk menambah angka 0 di belakang untai apapun yang kamu tuliskan di sana. Untuk melihat kerja mesin ini, tekan tombol ▶. Setelah selesai, kamu dapat menekan tombol ↩ untuk mengulang. Kamu juga dapat mengganti-ganti sendiri untai, status, maupun program yang ada di sana.
Apakah mesin ini menghitung sesuatu?
Perhatikan bahwa 101 dalam bilangan biner bernilai sama dengan 5 dalam bilangan desimal, sementara 1010 dalam bilangan biner bernilai sama dengan 10 dalam bilangan desimal. Artinya, mesin penambah ekor 0 ini sekaligus berfungsi sebagai mesin pengali 2 jika setiap simbol pada pita ditafsirkan sebagai bilangan.
Jika kita menganggap bahwa simbol-simbol awal yang tertulis pada pita sebagai input, dan simbol-simbol akhir pada pita sebagai output, kita telah menciptakan sebuah kalkulator sederhana. Masukkan input 10010 (18 desimal), maka output yang dihasilkan adalah 100100 (36 desimal), dan seterusnya.
Cara kita menuliskan bilangan sehari-hari adalah dengan menggunakan sistem desimal. Sistem desimal menggunakan 10 macam simbol: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Setelah 9 sudah tidak ada simbol lagi, karena itu kita mengulang dari 0, dengan menambahkan 1 di sebelah kirinya, menjadi 10. Setelah menghitung hingga 19, kita akan kehabisan simbol lagi. Karena itu kita mengulang dari 0 dan melanjutkan angka di sebelah kirinya, menjadi 20.
Dalam sistem biner, kita hanya memiliki 2 macam simbol: 0 dan 1. Sehingga ketika mencacah, kita mencacah dari 0, 1, kemudian kehabisan simbol. Karena itu simbol diulang dari 0, dan ditambahi 1 di sebelah kirinya menjadi 10. Demikian seterusnya.
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, ...
Untuk menerjemahkan bilangan biner ke desimal, caranya adalah dengan mengalikan masing-masing digit dengan
Bilangan biner 110101, misalnya, dapat diterjemahkan dengan cara:
| digit | 1 | 1 | 0 | 1 | 0 | 1 |
|---|---|---|---|---|---|---|
| posisi | 5 | 4 | 3 | 2 | 1 | 0 |
| pengali | 25 | 24 | 23 | 22 | 21 | 20 |
Dengan demikian bilangan biner 110101 sama dengan desimal 53.
Mesin-mesin Turing yang lebih rumit dapat dibentuk menggunakan instruksi yang lebih rumit juga. Kamu dapat membuat mesin untuk memeriksa apakah bilangan input adalah bilangan prima atau bukan. Kamu juga dapat membuat mesin untuk menghitung segala hal yang dapat dihitung kalkulatormu.
Agar lebih jelas lagi, di bawah ini ada beberapa tautan video penjelasan mengenai mesin Turing.
Alan Turing: Crash Course Computer Science #15
Turing Machines Explained Visually
How Turing Machines Work - BitMerge
Terdapat juga aplikasi web dan Android yang dapat kamu gunakan untuk mengeksplorasi mesin Turing.
Berikutnya: Contoh-contoh lainnya