Prinsip penomoran

Hal yang kita lakukan sebelumnya sebenarnya adalah menomori setiap elemen himpunan dengan bilangan asli.

Perhatikan bahwa selama kita dapat menomori anggota himpunan menggunakan nomor urut dari 1, 2, 3, 4, 5, dan seterusnya, maka himpunan tersebut akan ternomori seluruhnya dengan bilangan asli, yang berarti banyak anggota himpunan tersebut adalah sama dengan banyak bilangan asli yang tersedia.

Jika setiap objek dalam sebuah himpunan tak berhingga dapat dinomori dengan bilangan asli secara berurutan, besarnya himpunan tersebut sama dengan bilangan asli.

Menomori bilangan bulat

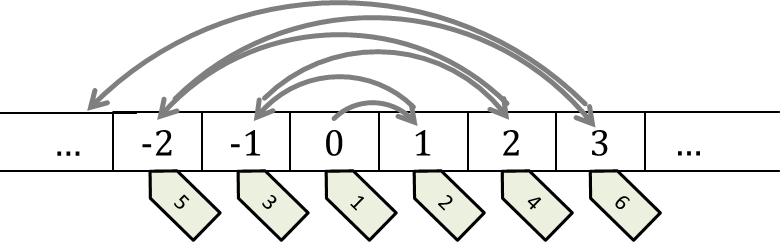
Dengan menggunakan prinsip ini, kita dapat menomori bilangan bulat dengan algoritma sebagai berikut:

1. Mulai dari bilangan 0, tandai sebagai nomor 1.
2. Cari bilangan pertama di sebelah kanan 0 yang belum dinomori, tandai sebagai nomor berikutnya.
3. Cari bilangan pertama di sebelah kiri 0 yang belum dinomori, tandai sebagai nomor berikutnya.
4. Ulangi langkah 2 dan 3 hingga kekekalan.

Dengan menjalankan algoritma tersebut, setiap bilangan bulat akan mendapat nomor tanpa kecuali, yang menunjukkan bahwa banyaknya bilangan bulat sama dengan banyaknya bilangan asli.

Berikutnya: Bilangan asli dan bilangan rasional