Postulat 5: Garis sejajar
Jika sebuah garis melalui dua garis lain, dan jumlah sudut dalam kedua garis tersebut pada sisi yang sama adalah kurang dari dua kali sudut siku-siku, maka kedua garis tersebut akan bertemu jika diperpanjang.
Berbeda dari postulat-postulat sebelumnya, postulat kelima ini tidak terlalu jelas. Kata-kata yang digunakan sulit dan bertele-tele. Namun untuk mencoba memahaminya, mari kita urai satu per satu yang dimaksudkan oleh postulat ini.
Pertama, postulat ini menyebutkan ada sebuah garis dan dua garis lain. Anggap garis p dan q di bawah ini sebagai dua garis lain tersebut.
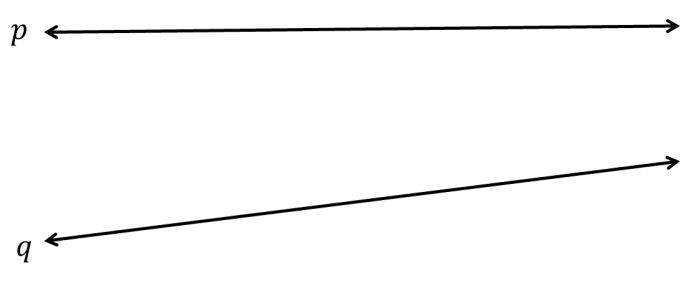
Garis pertama justru kita gambar belakangan, yaitu garis r, yang melalui dua garis lain tersebut, yaitu garis p dan q.

Terlihat bahwa garis r akan membentuk dua sudut dalam terhadap kedua
garis lain tersebut. Sudutnya kita beri nama α dan β. Kondisi yang
dibicarakan dalam postulat ini adalah ketika
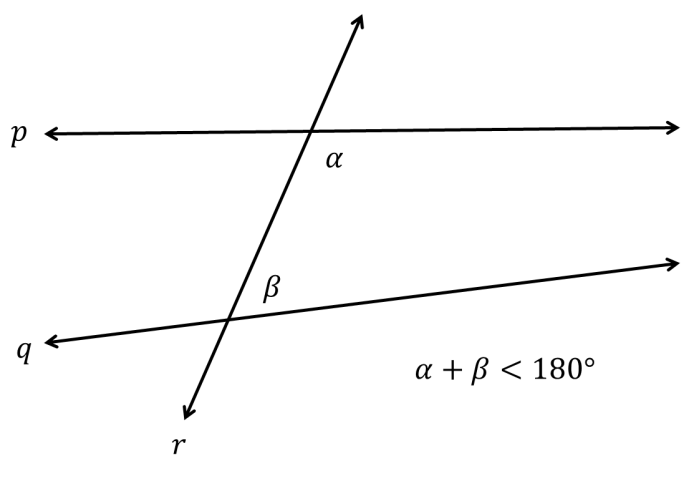
Jika syarat tersebut dipenuhi, postulat ini menjanjikan bahwa dua garis tersebut (p dan q) akan bertemu suatu saat jika diperpanjang terus.
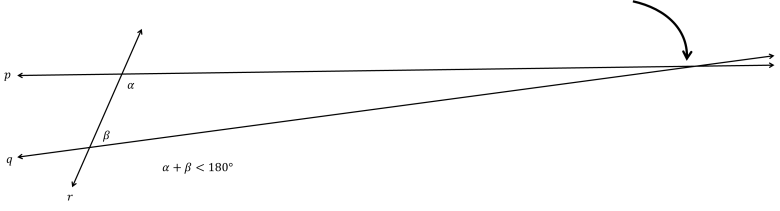
Postulat 5 John Playfair
Seperti yang telah kamu baca di atas, postulat kelima ini tidak sejelas keempat postulat sebelumnya. Seorang ahli matematika bernama John Playfair menyederhanakan postulat kelima ini.
Diberikan sebuah garis dan sebuah titik di luar garis itu, terdapat tepat satu garis yang melalui titik tersebut yang sejajar garis yang semula.
Jadi terdapat sebuah garis, misalnya kita sebut sebagai p, dan sebuah titik T yang di luar garis p.

Postulat ini mengatakan bahwa kamu bisa membuat garis yang sejajar dengan p, tetapi sekaligus melewati T. Misalnya pada gambar di bawah ini garis tersebut adalah garis q.
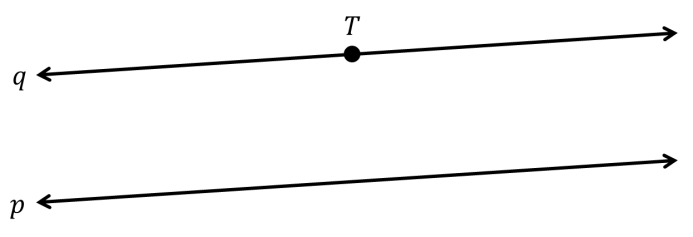
Postulat ini menjanjikan bahwa garis yang bisa kamu buat hanya satu. Tampaknya memang demikian. Kalau kita coba membuat garis lain seperti pada gambar di bawah ini:
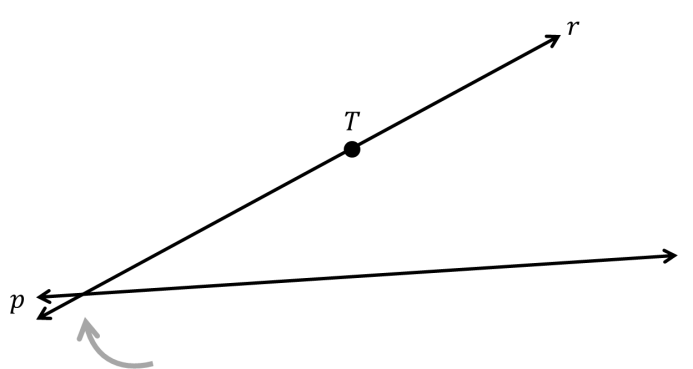
Garis r memang melewati T, tetapi tidak sejajar dengan p. Akibatnya, r dan p pasti berpotongan.
Sekarang misalnya kamu membuat garis lain (s) yang melewati T juga, sekaligus sejajar p.
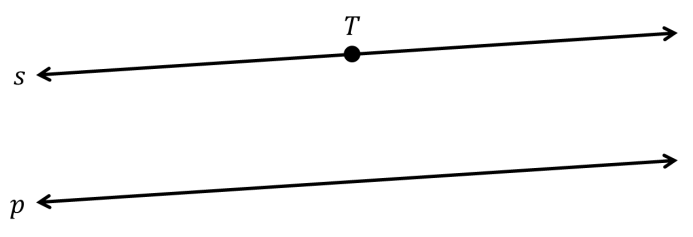
Terlihat bahwa garis s dan q tidak ada bedanya. Karena keduanya sama, berarti garis yang bisa dibuat melalui T sekaligus sejajar dengan p hanya satu, apapun namanya.
Sampai di sini, kita telah memiliki lima postulat yang siap dipakai untuk membangun geometri.
Ruas garis lurus dapat dibentuk dari satu titik ke titik yang lain.
Ruas garis dapat diperpanjang sepanjang-panjangnya.
Lingkaran dapat dibentuk menggunakan ruas garis sebagai jari-jari, dan salah satu titik ujungnya sebagai pusat lingkaran.
Semua sudut siku-siku adalah kongruen.
Jika sebuah garis melalui dua garis lain, dan jumlah sudut dalam kedua garis tersebut pada sisi yang sama adalah kurang dari dua kali sudut siku-siku, maka kedua garis tersebut akan bertemu jika diperpanjang.
Berikutnya: Proposisi-proposisi