Himpunan tak berhingga

Kedua barisan berikut ini dapat diteruskan tanpa pernah berhenti.

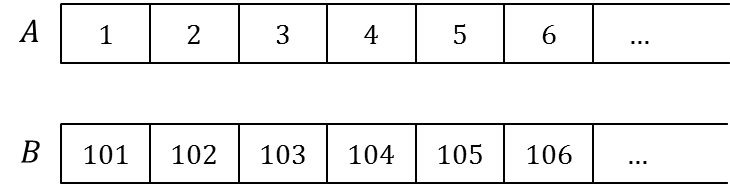
Manakah yang lebih banyak mengandung bilangan, barisan A atau B? Sekilas tampaknya A, bukan? Karena tampaknya barisan B tidak memiliki bilangan 1 hingga 100, yang dimiliki oleh A. Jadi tampaknya A memiliki kelebihan 100 bilangan dibandingkan B.

Namun orang juga dapat memberikan argumen bahwa kedua barisan tersebut memiliki banyak bilangan yang sama, karena toh keduanya sama-sama tak berhingga.

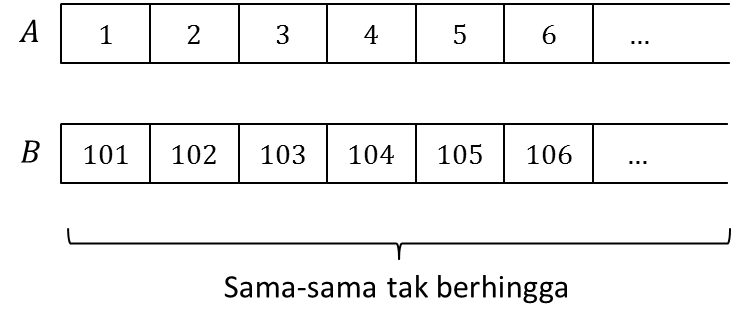
Bagaimana ini? Yang manakah yang benar? Mengapa bisa ada dua pendapat yang bertentangan untuk satu hal yang sama?

Permasalahannya terletak pada ungkapan “meneruskan tanpa pernah berhenti” yang tidak terdefinisi dengan baik. Kita menggunakan pengalaman kita sehari-hari untuk menilai sesuatu yang tidak akan kita jumpai sehari-hari.

Kita memerlukan strategi lain untuk membandingkan banyak anggota kedua himpunan. Kita akan mulai dari himpunan yang lebih sederhana. Manakah yang lebih banyak, laki-laki di sebelah kiri atau perempuan di sebelah kanan?

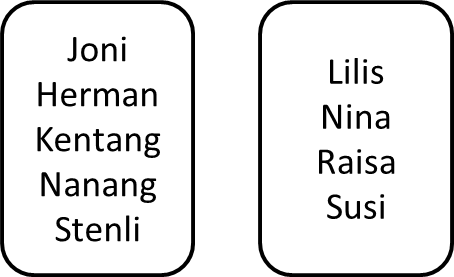
Biasanya, kita akan menghitung satu per satu. Ada 5 nama dalam daftar laki-laki, dan 4 nama dalam daftar perempuan.

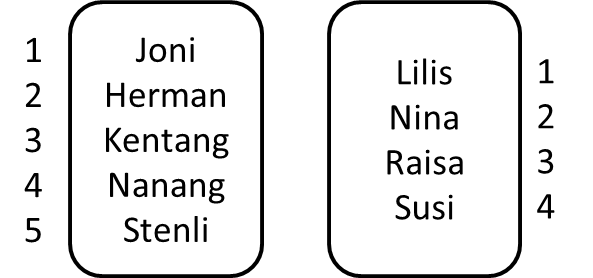
Karena daftar sebelah kiri 5, sedangkan yang kanan 4, dan 5 lebih dari 4, berarti dapat disimpulkan bahwa daftar kiri mengandung lebih banyak nama.

Namun cara ini tidak dapat kita terapkan untuk daftar yang terdiri dari tak berhingga nama. Karena, menghitung daftar yang berisi tak berhingga anggota takkan pernah selesai dilakukan, dan toh pada akhirnya (jika selesai), hasilnya sama-sama tak berhingga.

Maka strategi yang digunakan harus lebih baik. Mari kita coba menyuruh para laki-laki untuk sebisa mungkin mencari pasangan dari para perempuan, dan sebaliknya. Pasangan ini tidak perlu didasarkan pada cinta sehingga siapa saja boleh berpasangan dengan siapa saja. Syaratnya hanya tidak boleh ada yang memiliki lebih dari satu pasangan. Dalam istilah relasi ini disebut sebagai relasi yang unik kanan dan unik kiri.

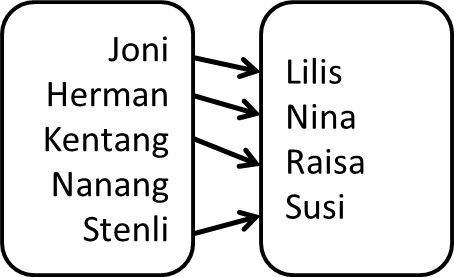
Terlihat bahwa daftar sebelah kiri memiliki satu laki-laki yang jomblo, yaitu Nanang. Karena terdapat laki-laki yang tidak memiliki pasangan, berarti jumlah laki-laki pasti lebih banyak dari yang perempuan.

Dalam kondisi apakah kedua daftar tersebut memiliki banyak nama yang sama? Kondisi tersebut adalah kondisi ketika semua laki-laki memperoleh pasangan, demikian juga sebaliknya semua perempuan juga memperoleh pasangan.

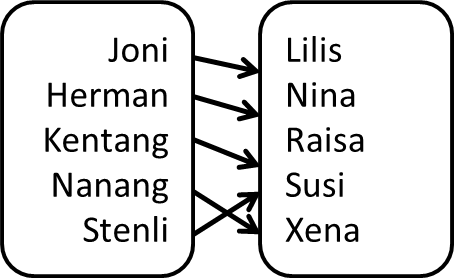
Dalam istilah relasi ini disebut sebagai relasi yang total kiri, total kanan, unik kanan, dan unik kiri. Istilah lainnya adalah fungsi bijektif.

Jadi, dua buah himpunan akan memiliki banyak anggota yang sama jika dan hanya jika dapat dibuat fungsi bijektif yang menghubungkan kedua himpunan tersebut.

Dua himpunan memiliki banyak anggota yang sama jika dan hanya jika dapat dibuat fungsi bijektif yang menghubungkan kedua himpunan tersebut.

Berarti dalam kasus dua barisan sebelumnya, kita dapat menguji: Apakah terdapat sebuah fungsi bijektif yang menghubungkan kedua himpunan tersebut? Jawabannya ada! Dengan menggunakan fungsi f\left( x \right) = x + 100, kita dapat memetakan 1 ke 101, 2 ke 102, 3 ke 103, dan seterusnya.

Setiap bilangan dalam A pasti memiliki pasangan di B (total kiri). Setiap bilangan dalam B pasti terpasangkan dengan A (total kanan). Tidak ada bilangan dalam A yang memiliki pasangan lebih dari satu (unik kanan), demikian juga sebaliknya (unik kiri). Fungsi f\left( x \right) = x + 100 bijektif untuk domain A dan kodomain B. Berarti, banyak anggota himpunan A dan B sama.

Perhatikan bahwa sebelumnya kita telah mempertimbangkan kesamaan keduanya. Masalahnya adalah pada pendapat awal kita (keduanya sama-sama tak berhingga), kita tidak memiliki dasar logika yang kuat.

Berikutnya mari kita coba membandingkan sejumlah himpunan.

Berikutnya: Bilangan asli dan bilangan genap