Geometri Hiperbolik
Geometri hiperbolik berlaku pada bidang yang lengkungannya seperti pelana kuda.


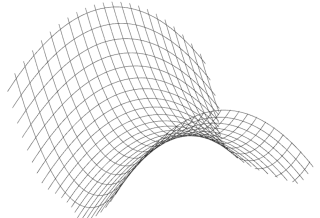
Bidang hiperbolik berupa permukaan lengkung yang bentuknya seperti pelana kuda. Gambar di atas memperlihatkan permukaan yang sama tetapi dari tiga sudut pandang yang berbeda. Di bawah ini kamu dapat mengamati bidang hiperbolik dari beberapa sudut pandang.
See the Pen Hyperbolic-space by Ari Prasetyo (@ariprasetyo) on CodePen.
Foto dari: goiwara - pixabay.com

Perbedaan dengan geometri eliptik
Untuk membedakannya dengan bidang geometri eliptik, kamu bisa membayangkan bahwa kamu berjalan di atas permukaan itu. Kamu bisa memiliki empat kemungkinan arah gerak seperti ini.

Di atas bumi, pergerakan kamu akan melengkung mengikuti kelengkunang permukaan bumi. Akibatnya, arah maju-mundur maupun kiri-kanan memiliki kecekungan yang sama, seperti pada gambar di bawah ini.

Kecekungan pada permukaan bola sama untuk keempat arah gerak.
Lain halnya dengan bidang hiperbolik. Perhatikan bahwa kecekungan untuk arah maju-mundur berlawanan dengan arah kiri-kanan.
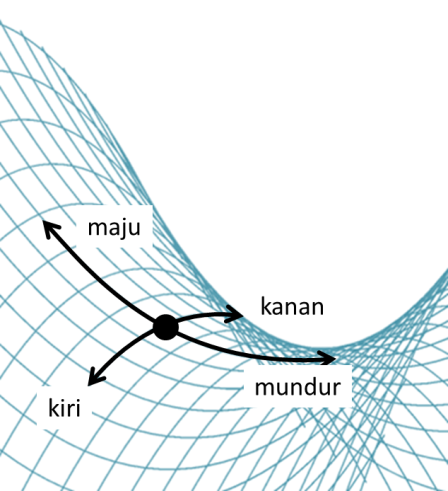
Dalam bidang hiperbolik, kecekungan untuk arah maju-mundur berlawanan dengan arah kiri-kanan.
Seperti sebelumnya, empat postulat pertama dalam geometri hiperbolik sama persis dengan geometri Euclid, tetapi postulat kelima berbeda.
Ruas garis lurus dapat dibentuk dari satu titik ke titik yang lain.
Ruas garis dapat diperpanjang sepanjang-panjangnya.
Lingkaran dapat dibentuk menggunakan ruas garis sebagai jari-jari, dan salah satu titik ujungnya sebagai pusat lingkaran.
Semua sudut siku-siku adalah kongruen.
Diberikan sebuah garis dan sebuah titik di luar garis itu, terdapat lebih dari satu garis yang melalui titik tersebut yang sejajar garis yang semula.
Bandingkan postulat 5 untuk ketiga macam geometri.
| Euclid | Diberikan sebuah garis dan sebuah titik di luar garis itu, terdapat tepat satu garis yang melalui titik tersebut yang sejajar garis yang semula. |
|---|---|
| Eliptik | Diberikan sebuah garis dan sebuah titik di luar garis itu, tidak ada garis yang melalui titik tersebut yang sejajar garis yang semula. |
| Hiperbolik | Diberikan sebuah garis dan sebuah titik di luar garis itu, terdapat lebih dari satu garis yang melalui titik tersebut yang sejajar garis yang semula. |
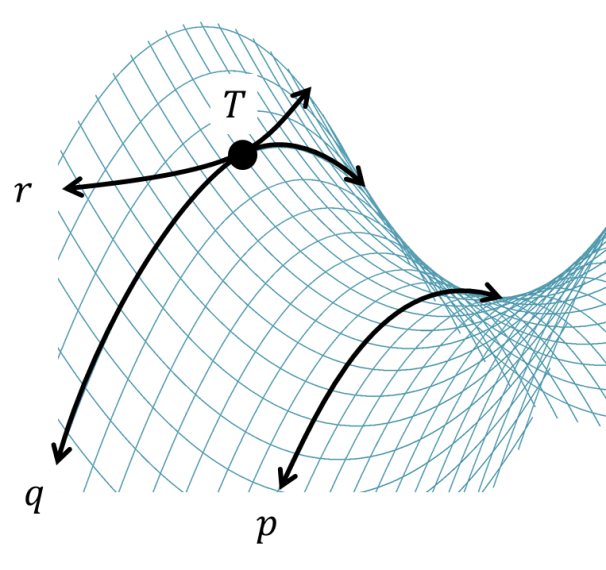
Sebagai contoh, di bawah ini adalah gambar garis p dan titik T di luar p. Garis q dan r sama-sama melalui titik T, tetapi tidak pernah memotong garis p, yang berarti q dan r sejajar dengan p.
Terdapat lebih dari satu garis yang sejajar p sekaligus melalui T, misalnya q dan r.
Berikutnya: Sudut segitiga kurang dari 180°