Interval terbatas dan tak terbatas

Interval yang sebelumnya kita bahas adalah interval yang terbatas. Berarti interval-interval tersebut memiliki batas kiri dan kanan.

Ada interval yang tak terbatas, yaitu yang salah satu atau kedua batasnya tak berhingga.

Interval yang terakhir, yaitu (-\infty, \infty) tidak memiliki notasi pertidaksamaan, tetapi memiliki alternatif penulisan. Karena pada dasarnya interval ini mengatakan bahwa t bisa bilangan real berapapun, maka interval tersebut bisa dituliskan sebagai:

Demikian juga ada interval yang tidak mungkin mengandung anggota. Misalnya:

Atau:

Karena tidak mungkin memiliki anggota, berarti interval-interval tersebut dapat dituliskan juga sebagai himpunan kosong.

Latihan

1. Nyatakan interval-interval berikut dalam bentuk garis bilangan notasi interval.

   1. 2 < a \leq 5
   2. - 3 \leq b < 4
   3. - 2 < c < 8
   4. - 1 \leq d \leq - \frac{1}{2}
   5. e < 9
   6. f \geq - 4

2. Ubahlah notasi interval berikut menjadi notasi pertidaksamaan dan garis bilangan.

   1. a \in \left\lbrack - 1,2 \right\rbrack
   2. b \in \left( 8,11 \right)
   3. c \in \left( \frac{- 1}{2}\sqrt{3},\frac{1}{2}\sqrt{3} \right\rbrack
   4. d \in \left\lbrack - \pi,\frac{8}{\pi} \right)
   5. e \in \left( - \infty,3 \right\rbrack
   6. f \in \left( 1,\infty \right)

3. Buatlah garis bilangan dan notasi interval yang dimaksudkan oleh masing-masing pertidaksamaan berikut.

   1. - 4 < a \leftarrow 2 atau - 1 \leq a < 3
   2. - 5 \leq b \leq 3 atau 4 \leq b < 5
   3. - 3 \leq c < 4 atau c \geq 6
   4. d \leftarrow 2 atau 0 \leq d \leq \sqrt{3}
   5. e \leq 4 atau e \geq 5
   6. f < 5 atau f > 5
   7. - 3 \leq g < 8 atau 8 < g < 11
   8. - 2 \leq h \leq 0 atau 0 \leq h < 6
   9. i \leq - 3 atau i \geq - 3
   10. 13 < j < 14
   11. k > 0
   12. l \le 4 atau 0 < l < 2 atau 4 \leq l < 5

4. Buatlah pertidaksamaan dan garis bilangan yang dimaksudkan oleh interval-interval di bawah ini.

   1. a \in \left\lbrack - 5, - 2 \right\rbrack \cup \left\lbrack 0,4 \right\rbrack
   2. b \in \left( - 7, - 3 \right\rbrack \cup \left\lbrack - 2, - 1 \right)
   3. c \in \left( - 4, - 2 \right\rbrack \cup \left( - 1,8 \right\rbrack
   4. d \in \left( - \infty,4 \right\rbrack \cup \left\lbrack 5,6 \right)
   5. e \in \left\lbrack 3,5 \right\rbrack \cup \left( 6,\infty \right)
   6. f \in \left( - \infty,8 \right) \cup \left\lbrack 9,11 \right)
   7. g \in \left\lbrack - 2,1 \right) \cup \left\lbrack \sqrt{3},\infty \right)
   8. h \in \left\lbrack 2,3 \right) \cup \left( 3,5 \right\rbrack
   9. i \in \left( - 4,3 \right\rbrack \cup \left( 3,8 \right\rbrack
   10. j \in \left\lbrack - 2,0 \right\rbrack \cup \left\lbrack 0,\pi \right)
   11. k \in \left( - 2,5 \right) \cup \left( 3,11 \right)
   12. l \in \left( - \infty,4 \right\rbrack \cup \left( 1,\infty \right)
   13. m \in \left( - \infty,\pi \right) \cup \left( \pi,\infty \right)
   14. n \in \left( - 2,4 \right\rbrack \cup \left\lbrack 5,6 \right) \cup \left( 6,\infty \right)
   15. o \in \left( - \infty,0 \right) \cup \left( 1,3 \right\rbrack \cup \left\lbrack 5,\infty \right)

5. Sederhanakan interval-interval berikut ini.

   1. a \in \left( - 4,8 \right) \cup \left( 6,11 \right)
   2. b \in \left( - \infty,5 \right\rbrack \cup \left( 5,\infty \right)
   3. c \in \left( - 2,8 \right) \cap \left( 4,11 \right)
   4. d \in \left\lbrack - 3,5 \right) \cap \left\lbrack 0,\infty \right)
   5. e \in \left( - \infty,12 \right\rbrack \cap \left( - 12,\infty \right)
   6. f \in \left( - 3,2 \right) \cap \left\lbrack 5,11 \right)

6. Sederhanakan interval-interval berikut ini.

   1. - 3 < a \leq 5 atau 3 \leq a < 7

   2. - 2 \leq b \leq 9 atau \pi < b < 11

   3. c > 7 atau c \leq 7

   4. d \geq 11 atau d \leq 18

   5. e \geq 6 atau 3 < e \leq 11 atau e < 0

   6. 3 < f \leq 5 dan 4 < f \leq 7

   7. g < 5 dan g \leq 9

   8. h > 7 dan h \leq 12

   9. i < 6 dan 3 < i < 5 dan i \leq 11

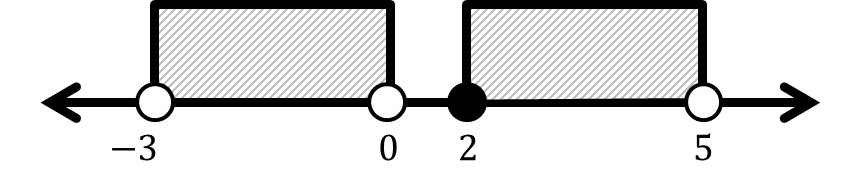
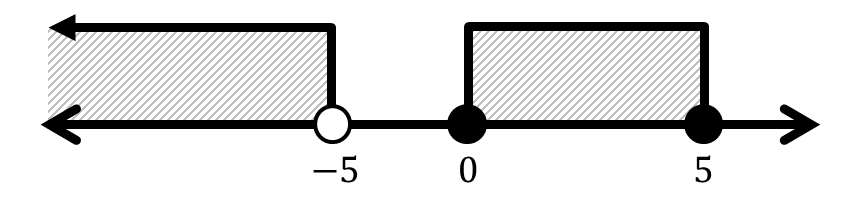
7. Tentukan notasi interval dan bentuk pertidaksamaan dari interval-interval berikut.

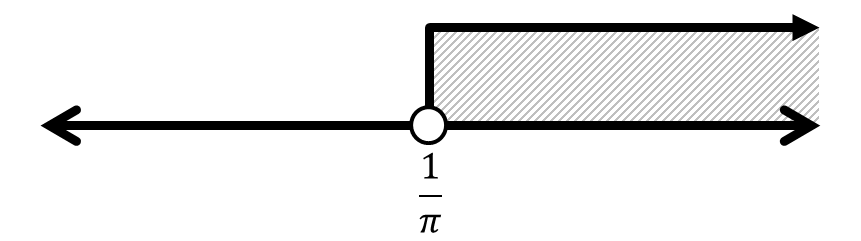
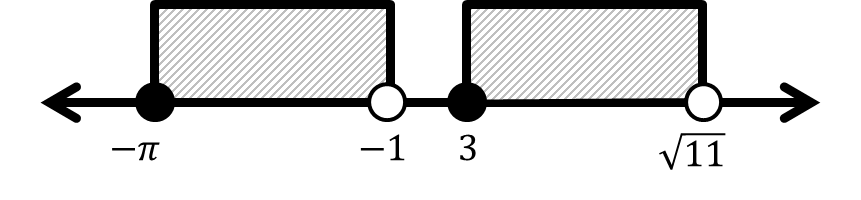
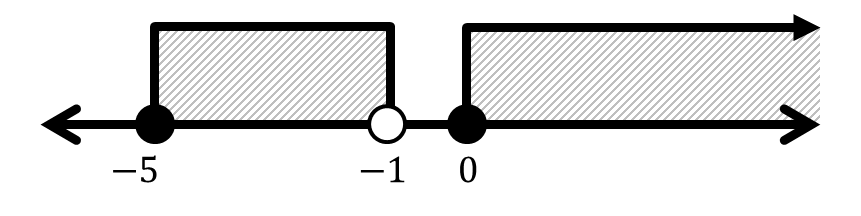
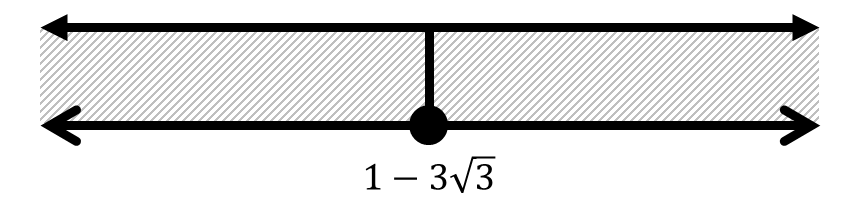
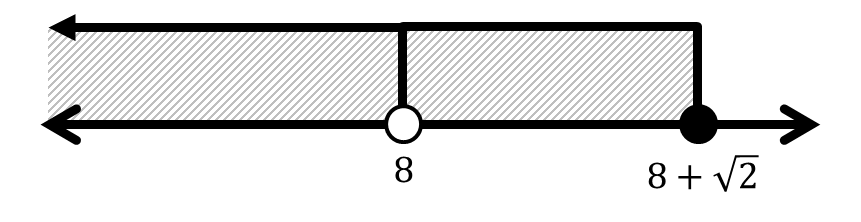
Berikutnya: Diskret dan Kontinu