Permutasi siklis : Ketika objek dalam susunan berkeliling

Suatu hari monster Bla, Bli, Blu, dan Ble duduk dalam posisi melingkar.

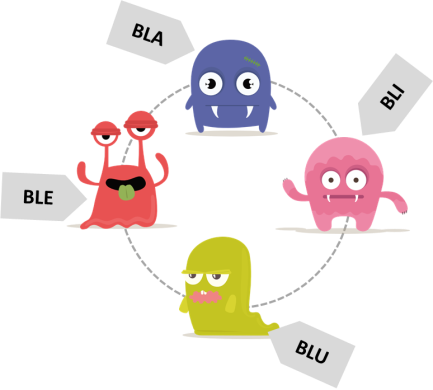
Perhatikan bahwa kalau mereka duduk dalam kedua macam posisi ini, kita dapat mengatakan bahwa mereka duduk dalam posisi yang sama.

Mengapa sama? Dalam posisi melingkar susunan yang dirotasi dianggap sama.

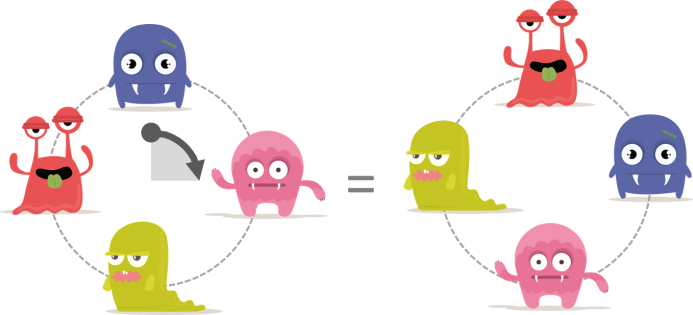
Untuk memahami hal ini, perhatikan posisi relatif mereka satu sama lain. Dalam gambar di bawah ini, Bli sedang duduk berseberangan dengan Ble. Sebelah kirinya adalah Blu, dan sebelah kanannya adalah Bla.

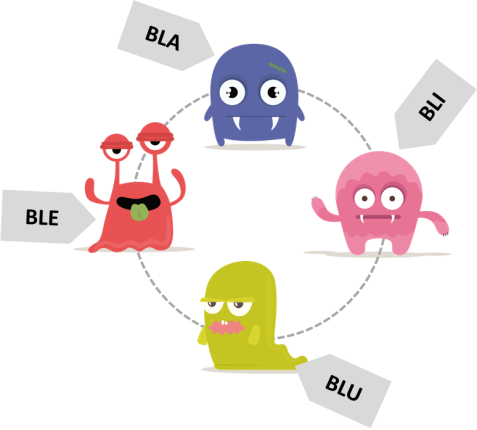
Seandainya kamu duduk dalam posisi Bli, kamu akan melihat posisi mereka seperti di bawah ini. Ble di seberang, Blu di kiri, dan Bla di kanan.

Sekarang seandainya mereka bertukar posisi seperti di bawah ini.

Kemudian kamu melihat lagi dari posisi Bli. Apa yang akan kamu lihat? Ble di seberang, Blu di kiri, dan Bla di kanan. Tepat seperti posisi sebelumnya.

Berarti, dalam posisi duduk melingkar posisi duduk yang dirotasi akan menghasilkan pemandangan yang sama bagi siapapun yang duduk di dalamnya. Kamu dapat mencobanya sendiri untuk posisi Bla, Blu, dan Ble.

Kalau begitu, posisi apa yang berbeda? Perhatikan posisi berikut.

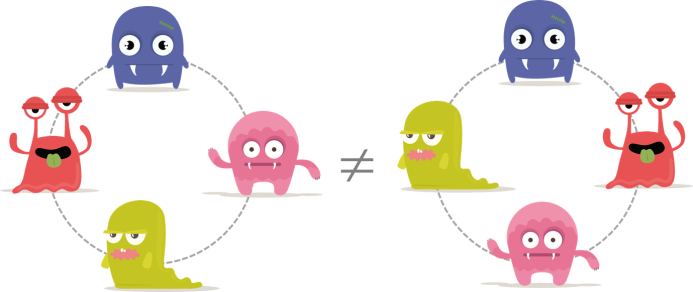
Mengapa kedua posisi di atas tidak sama? Kamu dapat memeriksa kembali dengan duduk di posisi Bli. Pada susunan sebelah kiri, kamu akan mendapati Ble di seberang, Blu di kiri, dan Bla di kanan. Seperti sebelumnya.

Namun pada susunan kedua, kamu akan mendapati bahwa yang ada di seberang bukanlah Ble, melainkan Bla. Sebelah kiri tetap Blu, tetapi sebelah kanan adalah Ble. Ini baru susunan yang berbeda!

Kalau begitu, dalam kasus posisi duduk melingkar, kamu harus menempatkan diri dalam posisi salah satu dari mereka, dan yang bertukar-tukar posisi adalah objek yang lain.

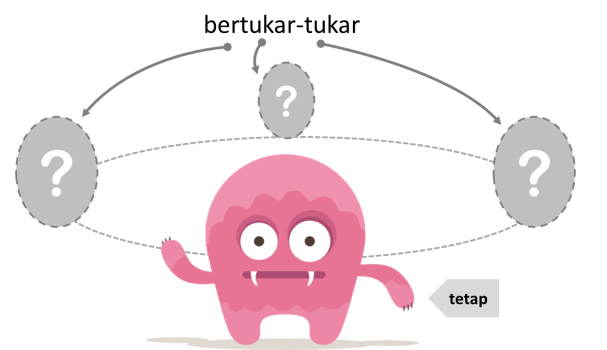
Ini disebut sebagai permutasi siklis. Permutasi siklis adalah permutasi terhadap susunan melingkar. Karena susunan melingkar dianggap sama ketika diputar-putar, maka permutasi baru dianggap berbeda ketika kamu menempatkan diri terhadap salah satu sudut pandang, kemudian melakukan permutasi terhadap sisa objek yang kamu lihat.

Sehingga, jika dalam permutasi linear banyaknya kemungkinan adalah n!, dalam permutasi siklis banyaknya kemungkinan adalah:

Latihan

1. Tentukan banyaknya permutasi jika Andi, Budi, dan Cacing duduk melingkar. Sebutkan semua susunan yang mungkin.

2. Tentukan banyaknya permutasi jika Acong, Bcong, Ccong, Dcong, dan Econg duduk melingkar. Tuliskan semua susunan yang mungkin.

3. Jeon Jeong-guk, Kim Tae-hyung, Park Ji-min, Kim Nam-joon, Jung Ho-seok, Min Yoon-gi, Kim Seok-jin hendak duduk makan dalam sebuah meja putar. Jika mereka duduk secara acak, terdapat berapa kemungkinan posisi mereka duduk?

4. Hendra memiliki suatu playlist dalam media playernya. Daftar lagunya adalah sebagai berikut:
   Iwak Peyek
   Sambalado
   Darah Muda
   Pusing Pala Barbie
   Sik Asik
   Alamat Palsu
   Senyum Membawa Luka
   Stasiun Balapan
   Sakitnya Tuh Di Sini
   Mirasantika

Lagu-lagu tersebut diputar berulang-ulang secara berurutan. Saat ini lagu yang diputar adalah Alamat Palsu. Jika teman Hendra mengetahui lagu-lagu yang diputar tersebut tetapi tidak tahu urutannya, berapa macam urutan yang mungkin yang dapat ia tebak?

1. Dalam sistem zodiak Cina, terdapat 12 binatang yang menandai tahun-tahun tertentu. Urutan yang disepakati adalah tikus, kerbau, macan, kelinci, naga, ular, kuda, kambing, monyet, ayam, anjing, dan babi. Tahun 2016 adalah tahun monyet, demikian juga tahun 2004, karena setiap tahun binatang-binatang ini secara bergiliran menandai tahun yang bersangkutan. Berapa banyakkah kemungkinan permutasi yang berbeda bagi zodiak Cina?

Berikutnya: Kombinasi