Menghitung banyaknya permutasi

Kalau kita perhatikan algoritma sebelumnya, setiap kali kita hendak mengisi sebuah tempat kosong, kita memiliki jumlah pilihan yang berubah.

Pertama-tama, karena jumlah kertasnya 3, berarti pilihan kita adalah 3.

Kemudian, setelah kita menempatkan satu kertas pada posisi pertama, hanya tersisa 2 pilihan bagi posisi kedua.

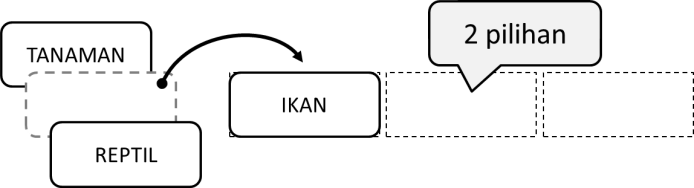
Terakhir, bagi posisi ketiga hanya tersisa 1 pilihan yang harus kita pilih.

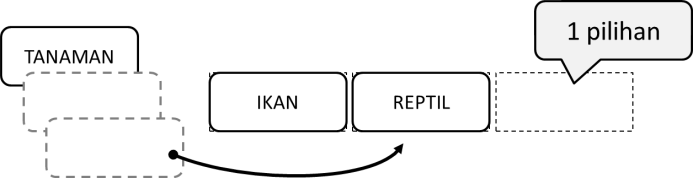
Sesuai aturan perkalian, banyaknya pilihan-pilihan tersebut tinggal kita kalikan untuk mendapatkan jumlah permutasi yang mungkin.

Kita dapat menggunakan cara seperti ini untuk kasus yang lebih umum.

Contoh

Hitunglah permutasi dari huruf-huruf ABCD.

Pertama, siapkan 4 tempat, karena ABCD terdiri dari 4 huruf.

Pada tempat pertama, kita dapat memilih huruf-huruf A, B, C, maupun D untuk mengisi.

Untuk tempat kedua, kita hanya boleh mengisinya dengan 3 huruf sisanya, karena 1 huruf sudah dipakai untuk mengisi tempat pertama.

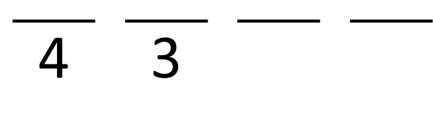
Sekarang 2 huruf sudah dipakai. Akibatnya, untuk tempat ketiga kita hanya dapat memakai 2 huruf. Demikian seterusnya hingga tempat terakhir.

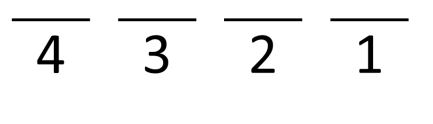
Keseluruhan permutasi dari ABCD berjumlah:

Latihan

1. Hitung banyaknya permutasi dari susunan huruf berikut:

   2. BAU
   3. BETON
   4. PISANG
   5. HAMSTERKU

2. Hitung banyaknya permutasi dari susunan angka berikut:

   7. 5931
   8. 19435
   9. 1842953

3. Budi, Herman, Susi, Lola, dan Joko hendak duduk sebaris di sebuah bangku panjang. Hitunglah banyak kemungkinan urutan mereka duduk.

4. Mona, Heru, Tongki, dan Banjo hendak lomba lari. Hitunglah banyak kemungkinan urutan juara 1, 2, dan 3.

Berikutnya: Faktorial