Hati-hati: Pembuktian yang sesat
Hingga kini, kita baru memiliki 3 aksioma dan 8 teorema. Masih ada 5 pernyataan lain (dari total 16) yang belum kita ketahui. Bahkan kita belum tahu apakah pernyataan-pernyataan tersebut dapat diketahui benar atau tidak.
Susi, apakah Amburegul mengungu Titanigo?
Ah, jelas tidak dong! Amburegul mengungu Bahrelway (A1). Kemudian Bahrelway tidak mengungu Titanigo (A3). Aturannya adalah kalau Amburegul mengungu Bahrelway, dan Bahrelway mengungu Titanigo, maka Amburegul mengungu Titanigo. Tapi Bahrelway tidak mengungu Titanigo. Berarti tidak cocok sama aturannya, kan? Kesimpulannya, Amburegul tidak mengungu Titanigo!
Oh... Begitu.
Argumen Susi sangat meyakinkan, bukan?
Tapi coba kita pikirkan kembali. Argumen susi adalah seperti ini.
Validkah argumen Susi? Coba periksa sekali lagi.
Argumen Susi tidak valid, walaupun kelihatan sangat meyakinkan. Inilah pentingnya kita mempelajari logika. Banyak argumen yang tampak meyakinkan ternyata tidak valid. Mari kita kembali melihat mengenai implikasi.
Kalau Joni kalah lomba, kita akan disiram air.
Dengan asumsi Sonya mengatakan hal yang benar, apa yang akan terjadi seandainya Joni menang lomba? Apakah Sonya dan teman-temannya tidak mungkin disiram air? Kalimat di atas hanya membicarakan keadaan Joni kalah lomba. Kalimat tersebut tidak membicarakan keadaan ketika Joni menang lomba. Artinya, Joni menang lomba tidak ada hubungan dengan mereka akan disiram air atau tidak. Berarti, masih mungkin untuk Sonya dan kawan-kawan disiram air.
Ini semua diakibatkan oleh natur kalimat implikasi. Ketika anteseden benar, konsekuen harus benar.

Namun ketika anteseden salah, konsekuen bisa benar maupun salah, karena tidak dibicarakan dalam kalimat tersebut.
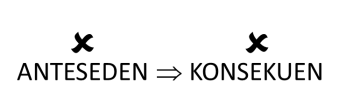
bisa juga

Dalam argumen Susi setelah aturan 3 disubstitusi (kita sebut dengan L1 saja):
ng(Amburegul, Bahrelway) ∧ ng(Bahrelway, Titanigo) ⇒ ng(Amburegul, Titanigo)
Antesedennya adalah:
- Anteseden L1
- ng(Amburegul, Bahrelway) ∧ ng(Bahrelway, Titanigo)
Padahal, yang kita tahu berdasarkan aksioma 1 dan 3:
ng(Amburegul, Bahrelway)
¬ ng(Bahrelway, Titanigo)
Yang menyebabkan anteseden menjadi salah.
- Anteseden L1
- ng(Amburegul, Bahrelway) (benar)
∧ ng(Bahrelway, Titanigo) (salah)
Konjungsi dua kalimat bernilai salah ketika salah satunya salah, sehingga L1 salah. Karena anteseden L1 salah, maka konsekuennya tak dapat ditentukan. Bisa benar, bisa salah.
ng(Amburegul, Titanigo) bisa benar, bisa salah.
Kalau begitu, ng(Amburegul, Titanigo) benar atau salah? Bagaimana kita menentukannya? Ataukah memang tak dapat ditentukan?
Ternyata dengan metode pembuktian langsung kita tak dapat menemukan jawabannya. Kita akan mencoba dengan pembuktian tak langsung.
Berikutnya: Pembuktian tak langsung