Namun kadang-kadang total
Sebutkan sifat-sifat yang dimiliki relasi berikut ini.

Relasi tersebut memiliki sifat:
Total kiri, karena setiap anggota H terhubung dengan anggota B.
Tidak total kanan, karena ada anggota B yang tidak terhubung dengan anggota H (yang mana?).
Tidak unik kanan, karena ada anggota H yang memiliki panah kanan bercabang (yang mana?).
Tidak unik kiri.
Jomblo dan selingkuh
Kamu bisa memahami konsep total dan unik dengan konsep ini: Jomblo dan selingkuh. Suatu relasi disebut total jika relasi itu tidak mengandung jomblo, dan disebut unik jika relasi itu tidak mengandung selingkuh.
TOTAL = NO JOMBLO
UNIK = NO SELINGKUH
Contohnya relasi berikut ini bersifat total kanan dan unik kiri tetapi tidak total kiri maupun unik kanan. Di bagian domain ada yang jomblo, berarti tidak total kiri. Ada yang selingkuh juga, berarti tidak unik kanan. Sebaliknya, di bagian kodomain tidak ada yang jomblo berarti total kanan. Juga tidak ada yang selingkuh berarti unik kiri. Alangkah indahnya jika setiap relasi asmara dalam suatu masyarakat bersifat total dan unik.
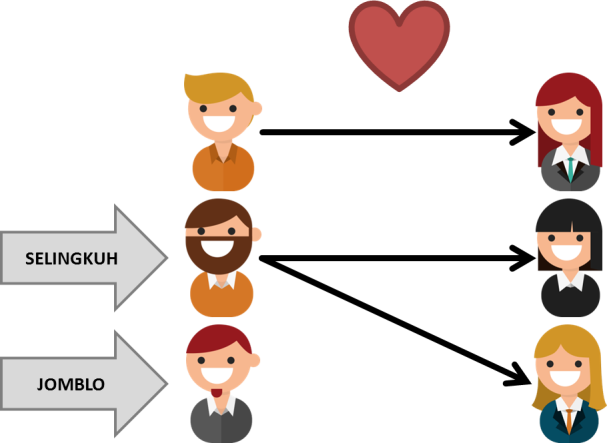
Catatan: Tidak ada maksud tertentu ketika menempatkan contoh yang selingkuh pada pihak laki-laki.
Pertanyaan: Apakah buku matematika yang mengandung kata selingkuh mengajarkan murid untuk selingkuh?
Berikutnya: Latihan