Diagram kartesius
Diagram kartesius pada hakikatnya adalah sama dengan tabel. Hanya saja, alih-alih menggunakan konsep sel sebagai perpotongan baris dan kolom, diagram kartesius menggunakan konsep koordinat sebagai perpotongan absis dan ordinat.
Pada umumnya, absis adalah garis mendatar, adalah tempat bagi domain. Sedangkan ordinat adalah garis tegak, tempat bagi kodomain.
Pertama, tuliskan domain di sumbu mendatar (horisontal).
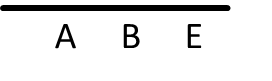
Berikutnya, tuliskan kodomain di sumbu tegak (vertikal).

Agar lebih jelas, biasanya kita memberikan grid. Ini tidak harus dilakukan, tetapi dapat memperjelas diagram terutama ketika jumlah domain dan kodomain sedikit.
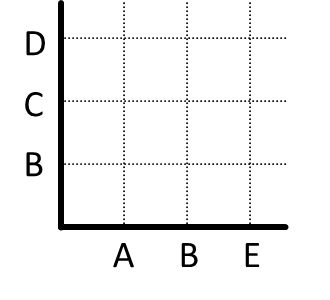
Karena (A, B) adalah penyelesaian dari kalimat terbuka tersebut, maka kita menempatkan titik yang bersesuaian. Kita cari A pada absis, dan B pada ordinat, lalu perpotongan dari keduanya adalah penyelesaian relasi tersebut.
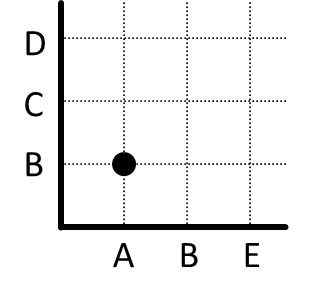
Lanjutkan dengan (A, C) dan (A, D).
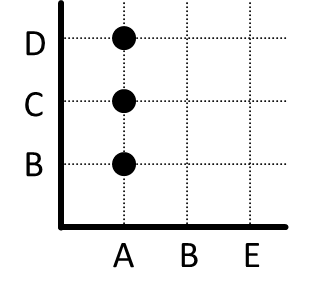
Lanjutkan lagi hingga seluruh penyelesaiannya tergambar dengan baik.

Latihan
A = {kucing, kelelawar, ikan}
B = {terbang, berlari, memanjat, berenang}
Jika relasi > didefinisikan dengan kalimat terbuka “semua x bisa y”, dengan x ∈ A, dan y ∈ B, tentukan himpunan penyelesaian, diagram panah, dan diagram kartesius untuk relasi tersebut.Dengan domain x∈{B, A, U} dan y ∈{K, L, M}, tentukan himpunan penyelesaian, diagram panah, dan diagram kartesius untuk setiap relasi berikut.
- x mendahului y dalam urutan abjad.
- x dan y sama-sama terdapat dalam kata BAUKAKI.
- x dan y sama-sama terdapat dalam kata KAKIKUDA.
- x dan y terkandung dalam nama saya. (maksudnya namamu sendiri)
- x dan y bersebelahan dalam kata KABUL.
- x dan y bersebelahan dalam kata BKTALTUM.
- x berada sebelum y dalam kata BALIKUM.
- x dan y sama-sama huruf konsonan.
- x dan y sama-sama huruf vokal.
- xy dapat dibaca karena mengandung huruf vokal.
Dengan domain x ∈{0, 1, 2} dan\ y ∈{-1, 0, 1}, tentukan himpunan penyelesaian, diagram panah, dan diagram kartesius untuk setiap relasi berikut.
x = y x > y x\ \leq \ y x\ \neq \ y - x = y x = 2y x + y = 0 x + y = 1 x = y + 1 x + 1 = y x\times y = 0 x\times y = 1 x\ \times \ y = 2 \frac{x}{y} = 1 x + y positif.x \cdot y positif.x \times y bilangan cacah.y dibagix tak bersisa.x dany kurang dari 2.x dany positif.x dany negatif.x atauy negatif.x atauy positif.- Jika
x = 0 ,y = 0 juga. - Jika
x > 0 ,y = - 1 .
Dengan domain x∈{-1, 0, 1} dan\ y ∈{0, 1, 2}, tentukan himpunan penyelesaian, diagram panah, dan diagram kartesius untuk setiap relasi berikut.
x = y x < y x \geq y x \neq y - x = y x = \frac{1}{2}y x + y = 0 x = 1 y = 2 x = 0 dany = 2 x = 1 atauy = 2 x = 1 ataux = 2 atauy = 0 x bukan 1 tapiy = 2 x^{y} negatifx^{y} tak terdefinisiy^{x} bilangan bulat\frac{x}{y} bilangan bulatx = ( - 1)^{y} x = \cos(\pi y) x = \sin(\pi y) x = \sin(\frac{\pi y}{2}) x = \sin( \frac{\pi}{2}(y + 1)) x = \tan( \frac{\pi}{4}y) x = \tan( \frac{\pi}{4}(y - 1)) \tan\(\frac{\pi}{4}x\) = y - 1
Hubungan antar relasi: Amatilah dua nomor sebelumnya untuk subsoal A hingga G. Apakah hubungan antara kedua relasi tersebut?
Berpikir induktif Amatilah diagram panah yang telah kamu buat. Perhatikanlah domain dan kodomainnya dan kelompokkan relasi tersebut menurut sifat-sifat yang serupa.
Berikutnya: Graf berarah