Untuk domain kontinu
Diberikan x, y ∈ Himpunan persegi dalam bidang Kartesius yang
memiliki sisi yang sejajar dengan sumbu X. Tentukan totalitas dan
keunikan relasi, x memiliki sisi yang juga adalah sisi y.
Dalam contoh-contoh sebelumnya, himpunan yang diberikan memiliki sedikit anggota. Namun persegi yang sifatnya seperti yang disebutkan di atas ada banyak sekali. Ada tak berhingga! Gambar di bawah ini hanya memperlihatkan empat di antaranya.

Tidak masalah. Kita tetap dapat menentukan sifat total dan uniknya.
Sifat total kiri berarti untuk setiap persegi x, ada persegi y yang memiliki sisi yang sama dengan x. Contohnya adalah:
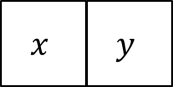

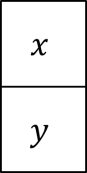
Jangan lupakan juga kasus khusus berikut ini, yaitu x dan y adalah persegi yang sama.
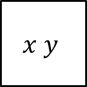
Apakah semua persegi yang sesuai definisi memiliki sifat tersebut? Tentu saja. Kita selalu dapat membuat persegi lain yang memiliki sisi yang sama dengan persegi apapun yang kita miliki.

Setidaknya, persegi itu sendiri juga memiliki sisi yang sama dengan dirinya sendiri. Ini berlaku untuk setiap persegi. Karena itu, relasi ini bersifat total kiri. Dengan cara yang sama, kamu dapat membuktikan bahwa relasi ini total kanan.
Selanjutnya, sifat unik kanan berarti untuk setiap persegi x, hanya boleh ada paling banyak satu persegi y yang mengandung sisi yang sama. Ini jelas tidak mungkin, karena dari gambar di atas, setidaknya ada satu persegi yang bisa memiliki lima persegi y yang berbagi sisi dengannya. Karena itulah relasi ini tidak bersifat unik kanan, yang juga dengan cara yang sama dapat dibuktikan bahwa relasi ini tidak unik kiri.
Berikutnya: Latihan