Graf berarah
Nah, kalau diagram-diagram sebelumnya bisa dipakai untuk keadaan domain dan kodomain berbeda, graf berarah tidak bisa. Dalam graf berarah domain dan kodomain harus sama.
Langkah-langkah menggambar graf berarah.
Contoh 1
Gambarkan graf berarah untuk relasi berikut:
x, y ∈ {Andi, Roy, Mefiboset}
Nama x lebih panjang dari nama y.
Pertama, gambarkan semua domain yang diberikan. Domainnya adalah {Andi, Roy, Mefiboset}, sehingga kita gambar tiga titik dengan tiga nama mereka.
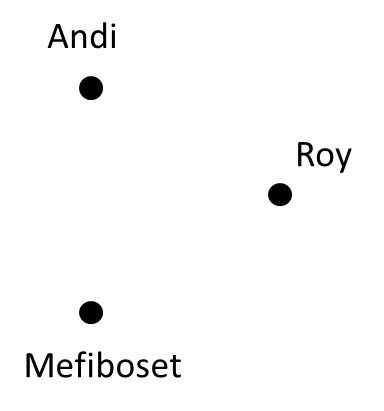
Dalam graf, posisi tidak penting. Kamu bisa menaruh Andi di sebelah kanan, atau menaruh semua nama tersebut dalam satu garis. Yang penting adalah kejelasan.
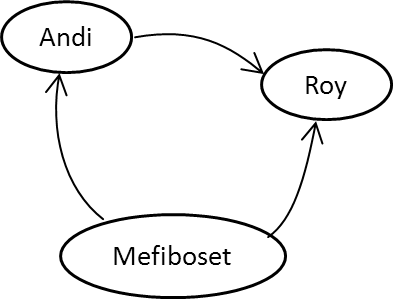
Berikutnya, beri tanda panah untuk objek yang berrelasi. Penyelesaian dari relasi tersebut adalah:
- (Andi, Roy) kita gambarkan sebagai panah dari Andi ke Roy.
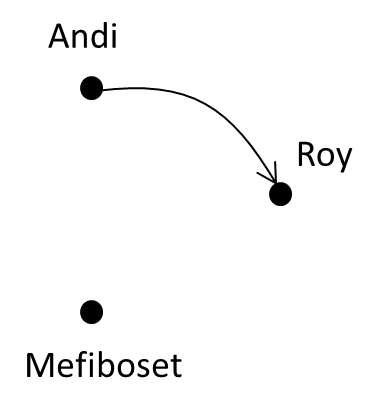
- (Mefiboset, Andi) kita gambarkan sebagai panah dari Mefiboset ke Andi.
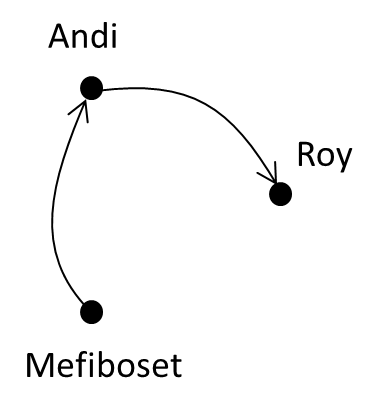
- (Mefiboset, Roy) kita gambarkan sebagai panah dari Mefiboset ke Roy.
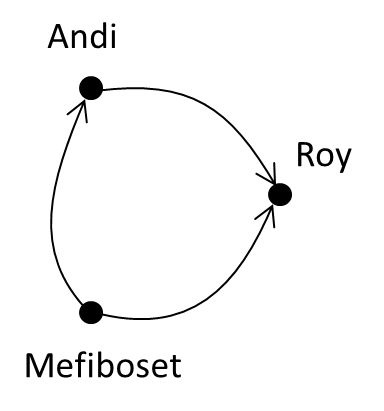
Kamu tidak harus menggambarka Andi, Roy, dan Mefiboset sebagai titik. Kamu boleh menggunakan bentuk yang lain. Ingat, yang penting adalah kejelasan.
| 
|
Contoh 2
Contoh berikutnya, diberikan domain\ {1, 2, 3, 4, 5}, dengan kalimat relasinya adalah, “x dikali y adalah bilangan ganjil.” Gambarkan sebagai graf berarah.
Pertama, gambarkan seluruh domainnya.
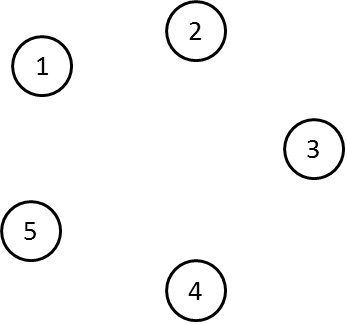
Kemudian, kita periksa satu per satu kemungkinan penyelesaiannya.
Jika x diganti 1 dan y diganti 3, kalimat tersebut berbunyi:
1 dikali 3 adalah bilangan ganjil.
Benar, karena
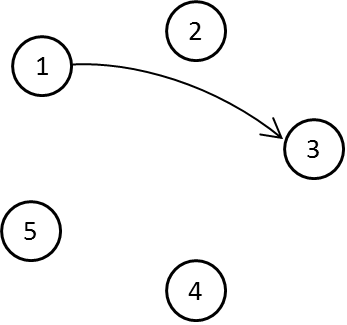
Namun, hal yang sebaliknya juga berlaku, bukan? 3 dikali 1 juga adalah bilangan ganjil. Berarti (3, 1) juga penyelesaian.
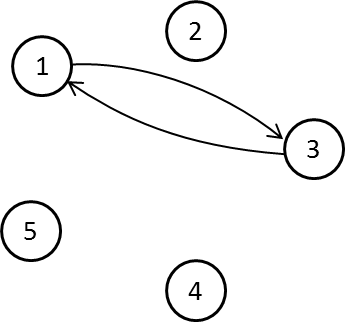
Karena berlaku bolak-balik, alih-alih menggambar dua panah, kita boleh (dan sangat dianjurkan) untuk gambarkan penyelesaian (1, 3) dan (3, 1) sebagai satu garis dengan dua kepala panah.

Dengan demikian orang yang membaca diagram tersebut akan langsung mengerti, bahwa 1 berelasi dengan 3, dan sebaliknya juga berlaku bahwa 3 berelasi dengan 1.
Berikutnya, tidak ada larangan bahwa x dan y tidak boleh sama. Apa yang terjadi ketika x dan y diganti 3? Kalimatnya akan menjadi:
3 dikali 3 adalah bilangan ganjil.
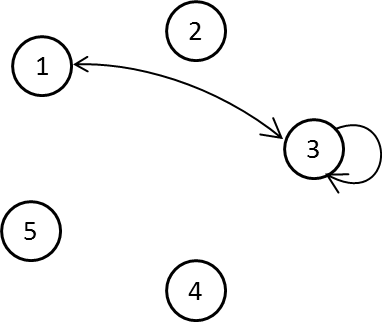
Dengan menelusuri penyelesaian-penyelesaian lainnya, kamu akan mendapatkan diagram lengkap seperti di bawah ini.
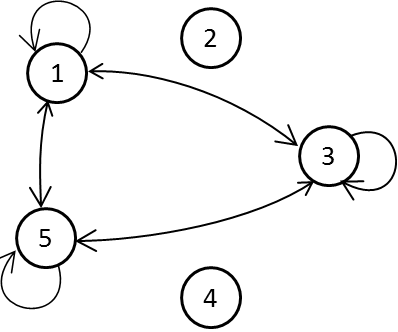
Dalam graf berarah posisi tidak penting. Kamu bisa menempatkan bulatan di mana saja, yang penting gambarnya jelas. Kasihan orang yang berusaha membaca diagram kalau kamu membuatnya rumit.
Latihan
Di bawah ini kamu diberi domain A, serta sejumlah relasi dalam domain A tersebut. Tentukan himpunan penyelesaiannya berdasarkan kenyataan sehari-hari, kemudian gambarkan relasinya sebagai graf berarah dan diagram kartesius.
A = {air, es, uap}
b(x, y) =
x dapat berubah menjadi y.
p(x, y) =
x dipanaskan dapat menjadi y.
A = {0°, 90°, 180°, 270°}
↰(x, y) =
sudut x diputar +90° menjadi y.
↷(x, y) =
sudut x diputar -180° menjadi y.
Catatan: Dalam posisi standar, sudut 0° adalah arah ke kanan.
Sudut positif berarti berlawanan jarum jam, dan negatif berarti searah jarum jam.
A himpunan 6 abjad pertama dalam bahasa Indonesia.
x < y =
x mendahului y dalam urutan abjad.
x & y =
x dan y sama-sama huruf vokal.
x ≅ y =
x dan y adalah huruf yang sama.
A himpunan semua bilangan cacah yang lebih kecil dari 5.
w(x, y) =
x+y lebih besar dari 4.
$(x, y) =
x = y – 2
*(x, y) =
x2 = y
<(x, y) =
x lebih kecil dari y
%(x, y) =
x dibagi y bilangan bulat.
Berikutnya: Menyajikan lebih dari satu relasi dalam sebuah diagram.