Tes garis

Line tests

Ada sebuah metode untuk menentukan totalitas dan keunikan relasi dalam diagram kartesius.

Tes garis vertikal

Vertical line test

Untuk mengidentifikasi relasi yang total kiri dan unik kanan, kita dapat menggunakan tes garis vertikal.

Total kiri

Apakah relasi ini total kiri?

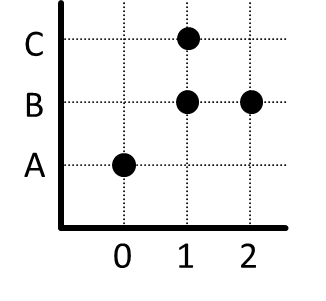
Untuk menentukan sifat total relasi ini, kita gunakan sebuah garis vertikal.

Letakkan garis ini pada masing-masing anggota domain, yaitu 0, 1, dan 2.

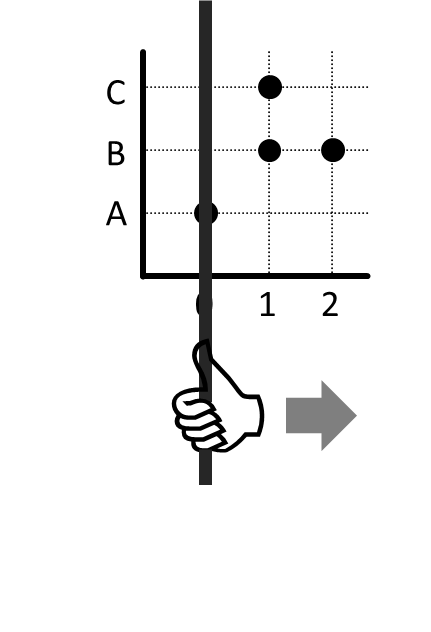
Ketika garis berada pada 0, terlihat bahwa garis tersebut melalui sebuah titik.

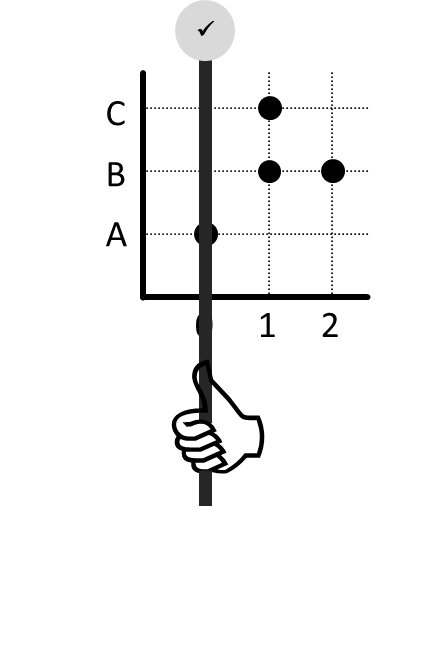
Demikian juga ketika garis berada di 1 dan 2.

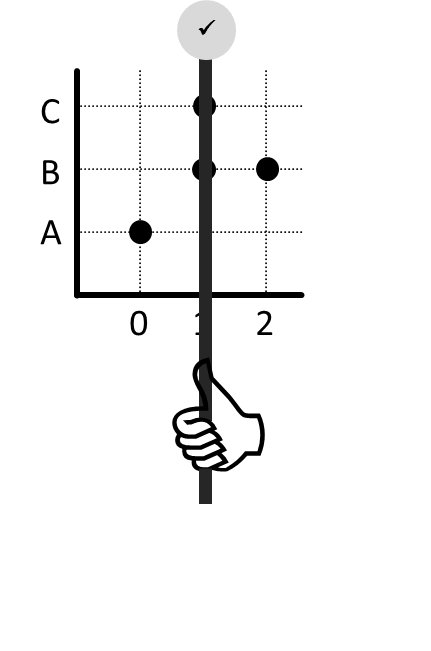
Karena setiap kali garis yang berada di anggota domain garis tersebut akan melalui titik dalam relasi, berarti relasi ini bersifat total kiri.

Unik kanan

Apakah relasi pada contoh sebelumnya juga unik kanan?

Tes garis vertikal juga dapat digunakan untuk menentukan keunikan.

Caranya seperti sebelumnya. Kunjungi masing-masing anggota domain kemudian periksa keadaan titik yang dilalui garis. Bedanya, pada pemeriksaan unik kanan tidak boleh ada titik yang terkena garis lebih dari satu.

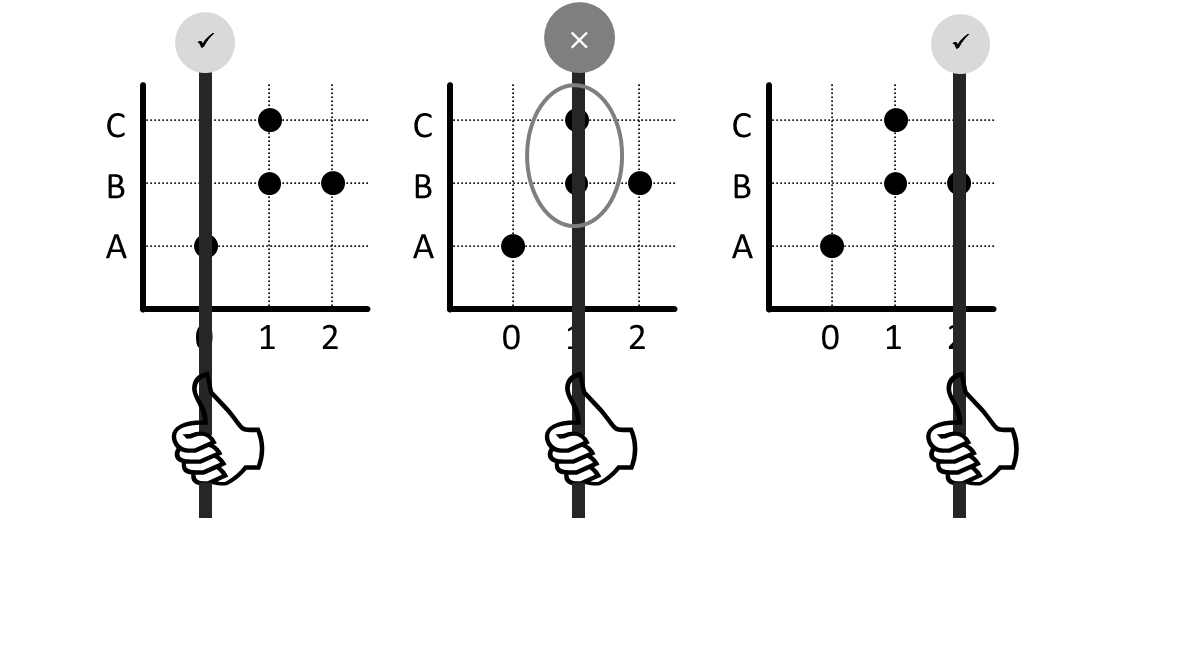
Pada contoh di atas, ketika garis vertikal diletakkan di 1 ternyata garis melalui dua titik, bukan hanya satu titik. Ini melanggar syarat unik kanan.

Berarti relasi ini bersifat total kiri tetapi tidak unik kanan.

Contoh

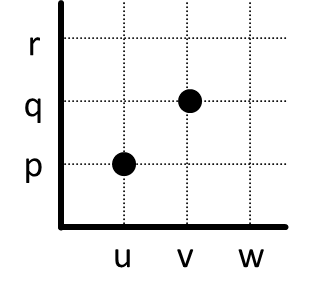
Mari kita kunjungi setiap anggota domain, yaitu u, v, dan w, menggunakan garis vertikal. Ternyata sewaktu kita mengunjungi w, garis vertikal tidak melewati titik sama sekali. Berarti relasi ini tidak total kiri.

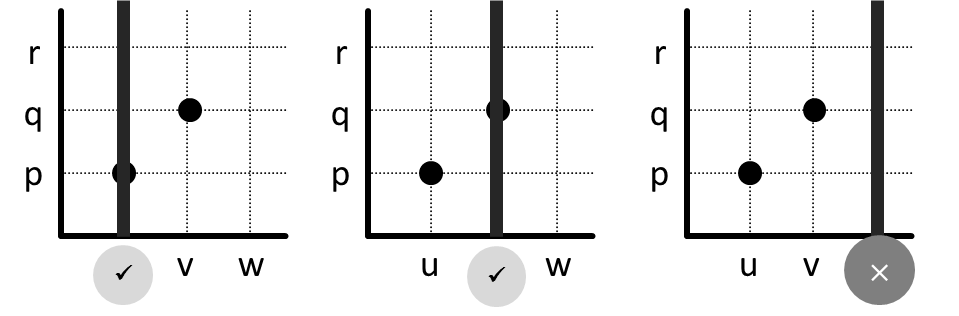
Namun ketika kita mencobanya untuk tes keunikan, ternyata berhasil untuk u, v, dan w. Tidak pernah garis vertikal melalui lebih dari satu titik. Artinya relasi ini bersifat unik kanan.

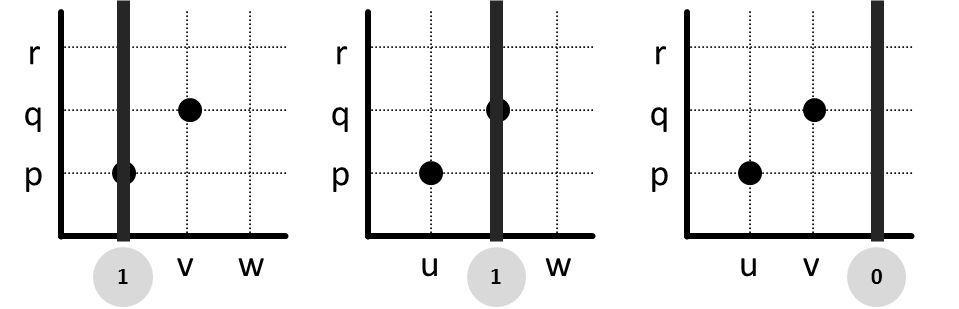
Kesimpulannya, relasi ini adalah tidak total kiri tetapi unik kanan.

Tes garis horisontal

Horizontal line test

Pada dasarnya tes garis horisontal sama dengan tes garis vertikal. Perbedaannya hanya pada arahnya saja. Karena garis yang digunakan horisontal berarti yang dikunjungi adalah kodomain. Dan karena tes dilakukan terhadap kodomain berarti tes ini akan mengidentifikasi total kanan dan unik kiri.

Contoh

Tentukan sifat-sifat yang dimiliki oleh relasi berikut ini.

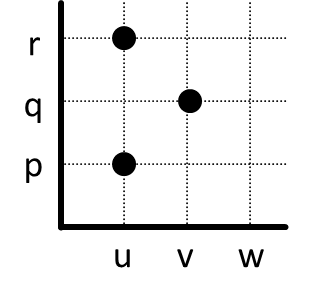
Dengan menggunakan garis horisontal, kita kunjungi masing-masing anggota kodomain.

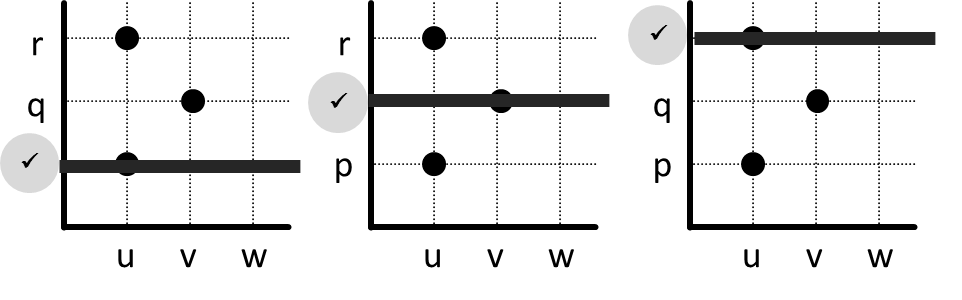
Ternyata ketika kita kunjungi p, q, maupun r, garis horisontal selalu melewati titik. Berarti relasi ini total kanan.

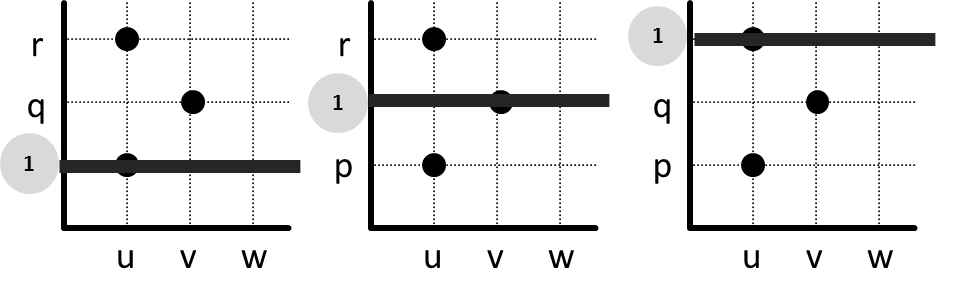
Terlihat juga ketika kita kunjungi p, q, maupun r, garis hanya melewati titik masing-masing 1. Sesuai sifat unik kiri, yaitu masing-masing anggota kodomain tidak terhubung lebih dari 1 anggota domain, berarti relasi ini unik kiri.

Jadi relasi ini bersifat total kanan dan unik kiri tetapi tidak total kiri dan tidak unik kanan. Buktikan dua sifat yang disebut terakhir.

Latihan

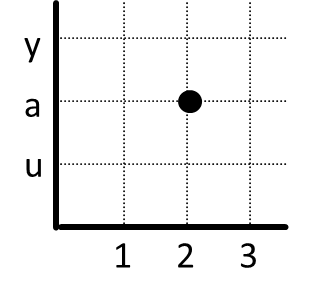
1. Tentukan totalitas dan keunikan relasi-relasi di bawah ini.

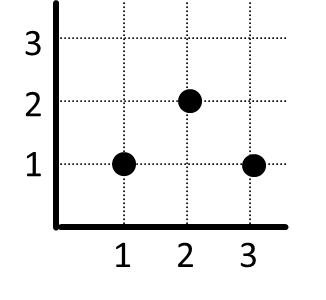
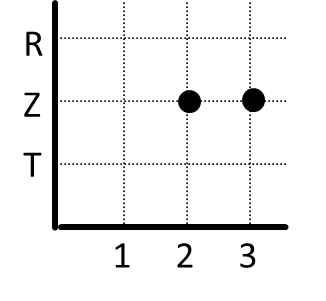
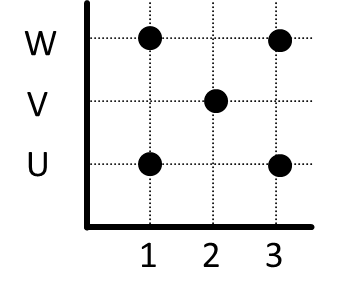
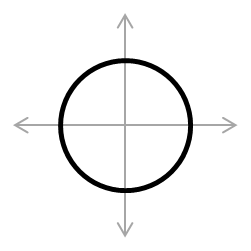
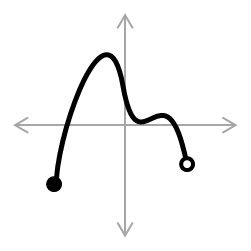
1. Diagram kartesius untuk bilangan real bersifat kontinu. Tentukan totalitas dan keunikan bagi masing-masing diagram kartesius berikut ini dalam domain bilangan real.

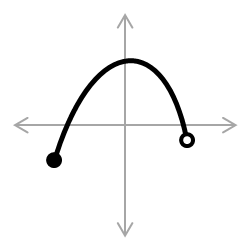
Berikutnya: Tes garis vertikal