Krucing dan mengungu

Dapatkah kamu menyimpulkan sesuatu berdasarkan hal yang tidak kamu mengerti dengan tuntas?

Susi
Herman, ke mana saja kamu? Seminggu kemarin kamu tidak masuk sekolah.
Herman
Iya, minggu lalu aku diculik alien.
Susi
Ha? Yang benar? Seperti apa mereka?
Herman
Mereka berbadan pendek. Mereka menceritakan tentang kebudayaan mereka tetapi aku tidak mengerti. Makanya aku dikembalikan lagi ke Bumi.
Susi
Seperti apa katanya?
Herman
Begini. Mereka menyebut diri mereka bangsa Krucing. Katanya, setiap Krucing bisa mengungu Krucing.
Susi
Mengungu? Apa itu?
Herman
Makanya itu. Aku tidak mengerti. Yang aku ingat, ada empat Krucing yang bertemu denganku. Namanya Amburegul, Bahrelway, Emeseyu, dan Titanigo.
Susi
Oh? Rasanya pernah dengar. Terus?
Herman
Amburegul mengungu Bahrelway. Bahrelway mengungu Emeseyu, tetapi tidak mengungu Titanigo.
Susi
Oh, begitu... (garuk-garuk kepala)
Herman
Ah, yang aku tahu tentang mengungu adalah begini. Setiap Krucing pasti mengungu diri sendiri.
Susi
Mengungu diri sendiri? Bagaimana caranya? Hmm.. sudahlah aku juga tidak tahu apa itu mengungu. Teruskan dulu.
Herman
Baik. Jadi Krucing itu...
Susi
Aha! Amburegul pasti mengungu diri sendiri!
Herman
Ha? Bagaimana kamu tahu? Kamu bahkan tidak tahu apa itu mengungu.
Susi
Lho, tadi kan kamu bilang bahwa setiap Krucing mengungu diri sendiri. Berarti, Amburegul, Bahrelway, Emeseyu, dan Titanigo, masing-masing mengungu diri sendiri dong!



  Setiap Krucing mengungu diri sendiri. Amburegul, Bahrelway, Emeseyu, dan Titanigo adalah Krucing. Berarti, mereka pasti mengungu diri sendiri.


  
  

Herman
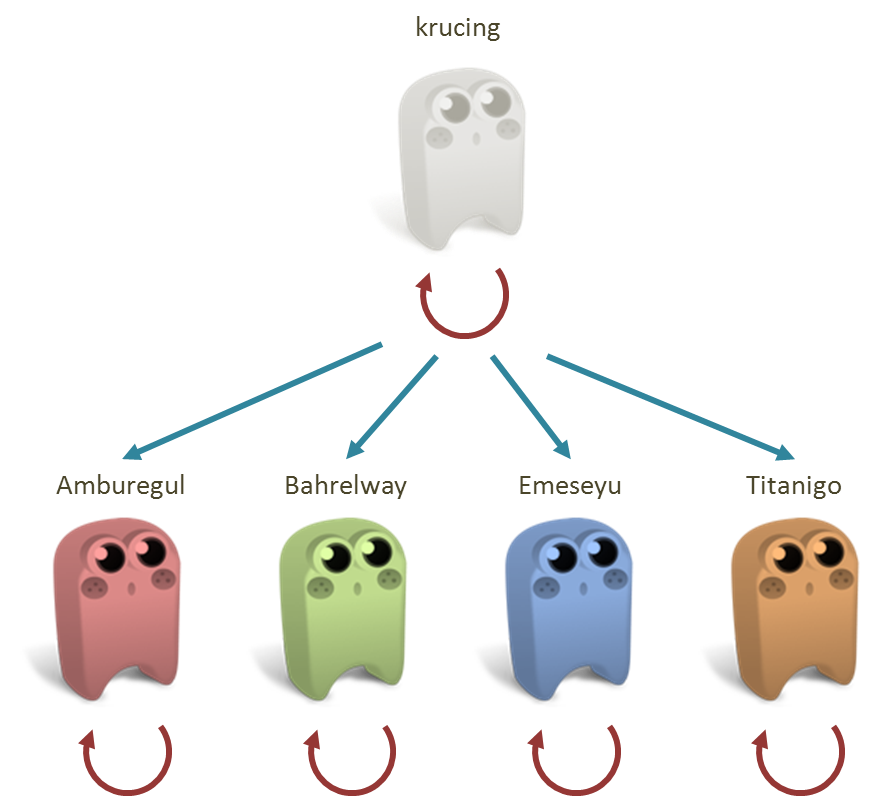
Benar juga ya! Kenapa tidak terpikirkan olehku!
Susi
Teruskan lagi.
Herman
Iya. Kemudian kalau seorang Krucing mengungu seorang Krucing lain, katakanlah, Krucing A mengungu Krucing B, berarti mereka saling mengungu. Kemudian, kalau Krucing A mengungu Krucing B, lalu si Krucing B ini mengungu Krucing C, maka Krucing A juga mengungu krucing C.
Susi
Aha! Pasti Amburegul mengungu Emeseyu!
Herman
Bagaimana kamu tahu?
Susi
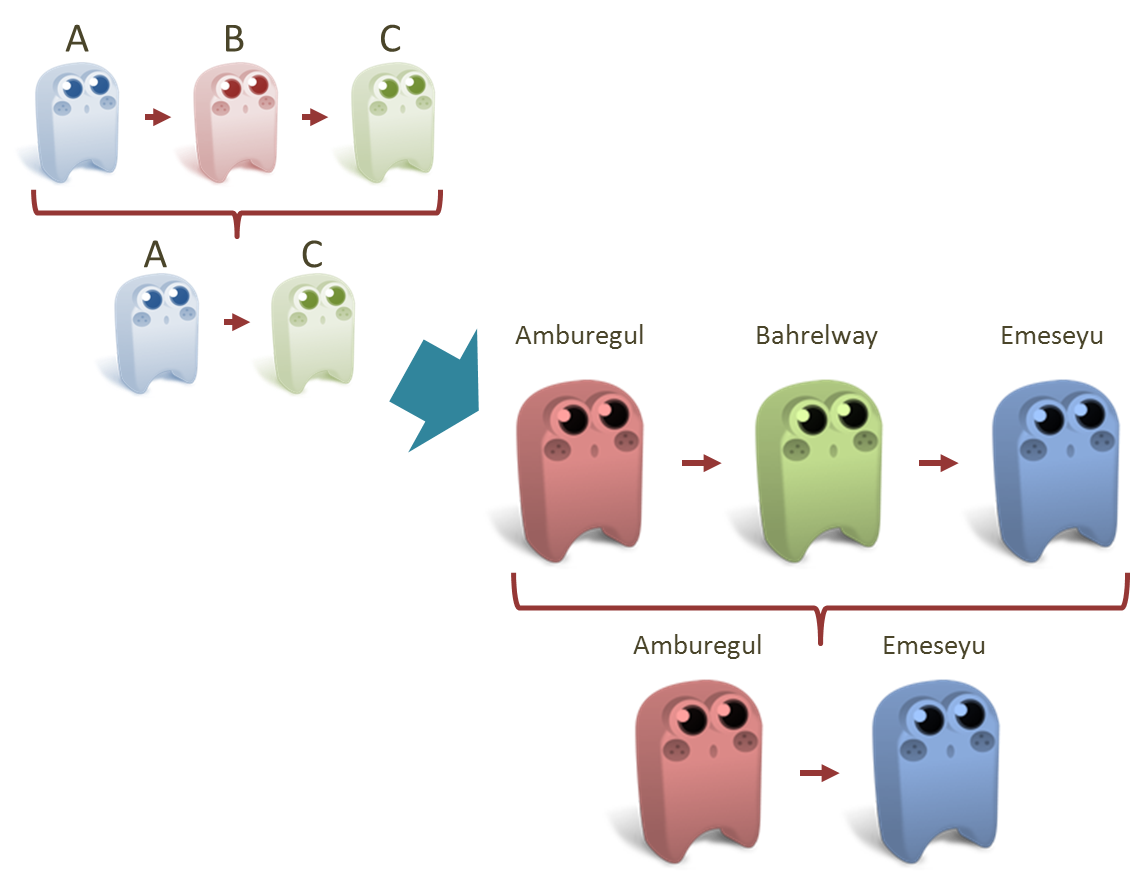
Sederhana. Kamu tadi bilang bahwa kalau A mengungu B, sedangkan B mengungu C, maka A juga mengungu C. Amburegul tadi mengungu Bahrelway kan? Lalu Bahrelway mengungu Emeseyu. Berarti, Amburegul pasti mengungu Emeseyu.
Herman
Oooh! Kamu pintar!
Susi
Emeseyu pasti juga mengungu Bahrelway.
Herman
Bagaimana?
Susi
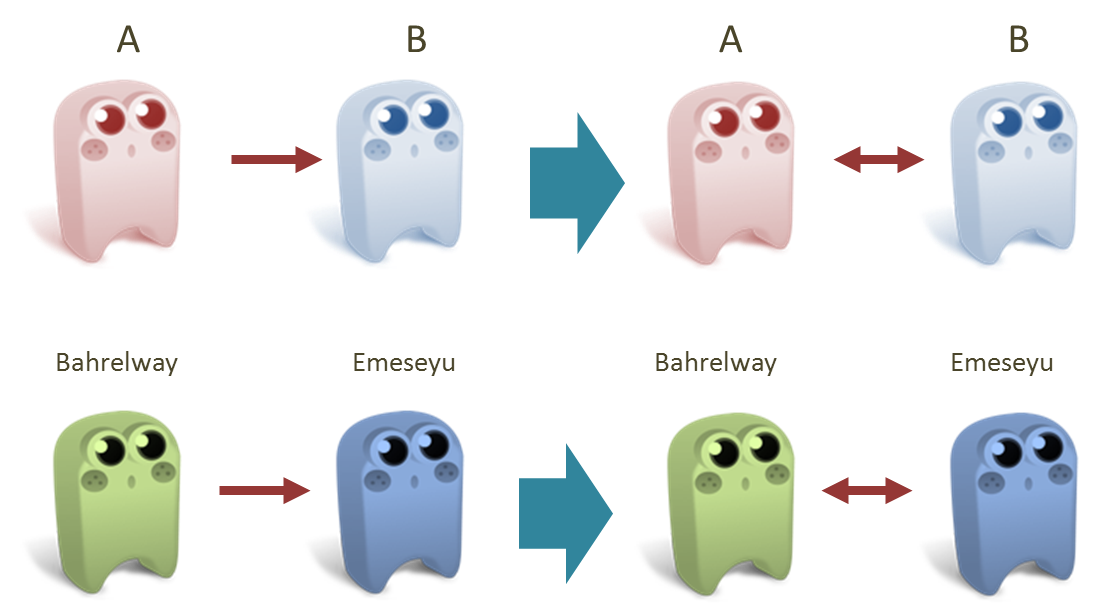
Iya, karena kalau A mengungu B, mereka saling mengungu. Bahrelway mengungu Emeseyu, kan? Berarti Emeseyu juga mengungu Bahrelway.
Herman
Ck... ck... ck...

Krucing: Transitif — Kalau Krucing A mengungu Krucing B, dan Krucing B mengungu Krucing C, berarti Krucing A juga mengungu Krucing C. Karena Amburegul mengungu Bahrelway dan Bahrelway mengungu Emeseyu, berarti Amburegul mengungu Emeseyu juga.

Krucing: Simetrik — Kalau A mengungu B, berarti mereka saling mengungu. Bahrelway mengungu Emeseyu, berarti mereka juga saling mengungu.

Dialog antara Herman dan Susi di atas adalah mengenai bangsa makhluk asing yang disebut Krucing. Herman dan Susi awalnya sama-sama tidak mengerti mengenai mengungu (demikian juga kita) karena konsep itu memang bukan dari dunia manusia. Namun yang mengherankan, sekalipun Susi tidak mengerti, bahkan ia tidak secara langsung mendengar penjelasan yang tidak jelas dari para Krucing, ia tetap dapat menarik kesimpulan.

Tidak hanya Susi, tetapi seharusnya kamu juga dapat menarik kesimpulan. Cobalah jawab pertanyaan-pertanyaan berikut dan jelaskan alasannya.

Apakah ini matematika?

Nah, sekarang kita masuk dalam pertanyaan yang lebih mendalam: Apakah konsep mengungu ini termasuk dalam matematika? Mari kita lihat.

Pertama, mengungu adalah sebuah konsep hubungan antara dua Krucing dengan aturan:

R1
Setiap Krucing mengungu diri sendiri.
R2
Kalau A mengungu B, mereka berdua saling mengungu.
R3
Kalau A mengungu B dan B mengungu C, maka A juga mengungu C.

Aturannya sih mirip matematika. Ada variabel A, B, dan C yang masing-masing bisa diganti dengan Amburegul, Bahrelway, Emeseyu, dan Titanigo. Namun apakah hanya karena ada variabel, maka ini disebut matematika?

Kemudian, perhatikan bahwa informasi yang dimiliki oleh Herman dan Susi diawali dengan tiga fakta berikut:

H1
Amburegul mengungu Bahrelway.
H2
Bahrelway mengungu Emeseyu.
H3
Bahrelway tidak mengungu Titanigo.

Dengan tiga fakta dan tiga aturan itu, Susi bisa menarik kesimpulan-kesimpulan lainnya:

S1
Amburegul mengungu diri sendiri.
S2
Bahrelway mengungu diri sendiri.
S3
Emeseyu mengungu diri sendiri.
S4
Titanigo mengungu diri sendiri.
S5
Amburegul mengungu Emeseyu.
S6
Emeseyu mengungu Bahrelway.

Dengan demikian, fakta yang mereka tahu, yang tadinya hanya 3, sekarang diperluas menjadi 9. Bahkan, kamu dapat meneruskannya untuk mendapatkan kesimpulan-kesimpulan lainnya lagi:

S1
Amburegul mengungu diri sendiri.
S2
Bahrelway mengungu diri sendiri.
S3
Emeseyu mengungu diri sendiri.
S4
Titanigo mengungu diri sendiri.
S5
Amburegul mengungu Emeseyu.
S6
Emeseyu mengungu Bahrelway.
S7
Bahrelway mengungu Amburegul.
S8
Emeseyu mengungu Amburegul.
S9
Titanigo tidak mengungu Bahrelway.
S10
Emeseyu tidak mengungu Titanigo.
S11
Titanigo tidak mengungu Emeseyu.
S12
Amburegul tidak mengungu Titanigo.
S13
Titanigo tidak mengungu Amburegul.

Apakah kamu sudah merasakan ada kemiripan dengan matematika?

Ngomong-ngomong, mengungu itu apa ya? Apakah Susi dapat menarik kesimpulan karena mengerti yang dikatakan Herman, teman sekelasnya? Namun tunggu dulu. Intermeso sebentar.

Hal yang sama berlaku untuk Susi dan Herman

Susi sekelas dengan Herman. Herman sekelas dengan Febi. Herman tidak sekelas dengan Bahdrun. Apa yang boleh disimpulkan dari informasi-informasi ini ya?

A1
Susi sekelas dengan Herman.
A2
Herman sekelas dengan Febi.
A3
Herman tidak sekelas dengan Bahdrun.
T1
Susi sekelas dengan dirinya sendiri.
T2
Herman sekelas dengan dirinya sendiri.
T3
Febi sekelas dengan dirinya sendiri.
T4
Bahdrun sekelas dengan dirinya sendiri.
T5
Susi sekelas dengan Febi.
T6
Febi sekelas dengan Herman.
T7
Herman sekelas dengan Susi.
T8
Febi sekelas dengan Susi.
T9
Bahdrun tidak sekelas dengan Herman.
T10
Febi tidak sekelas dengan Bahdrun.
T11
Bahdrun tidak sekelas dengan Febi.
T12
Susi tidak sekelas dengan Bahdrun.
T13
Bahdrun tidak sekelas dengan Susi.

Kamu dapat melihat bahwa ternyata sistem informasi mengenai sekelas ini mirip dengan mengungu.

	mengungu	sekelas
Informasi awal	Amburegul mengungu Bahrelway.	Susi sekelas dengan Herman.
	Bahrelway mengungu Emeseyu.	Herman sekelas dengan Febi.
	Bahrelway tidak mengungu Titanigo.	Herman tidak sekelas dengan Bahdrun.
Aturan	Setiap krucing mengungu dirinya sendiri.	Setiap murid sekelas dengan dirinya sendiri.
	Kalau A mengungu B, mereka berdua saling mengungu.	Kalau A sekelas dengan B, mereka berdua akan saling sekelas.
	Kalau A mengungu B, dan B mengungu C, maka A juga mengungu C.	Kalau A sekelas dengan B, dan B sekelas dengan C, berarti A juga sekelas dengan C.
Kesimpulan-kesimpulan	Amburegul mengungu diri sendiri.	Susi sekelas dengan dirinya sendiri.
	Bahrelway mengungu diri sendiri.	Herman sekelas dengan dirinya sendiri.
	Emeseyu mengungu diri sendiri.	Febi sekelas dengan dirinya sendiri.
	Titanigo mengungu diri sendiri.	Bahdrun sekelas dengan dirinya sendiri.
	Amburegul mengungu Emeseyu.	Susi sekelas dengan Febi.
	Emeseyu mengungu Bahrelway.	Febi sekelas dengan Herman.
	Bahrelway mengungu Amburegul.	Herman sekelas dengan Susi.
	Emeseyu mengungu Amburegul.	Febi sekelas dengan Susi.
	Titanigo tidak mengungu Bahrelway.	Bahdrun tidak sekelas dengan Herman.
	Emeseyu tidak mengungu Titanigo.	Febi tidak sekelas dengan Bahdrun.
	Titanigo tidak mengungu Emeseyu.	Bahdrun tidak sekelas dengan Febi.
	Amburegul tidak mengungu Titanigo.	Susi tidak sekelas dengan Bahdrun.
	Titanigo tidak mengungu Amburegul.	Bahdrun tidak sekelas dengan Susi.

Jadi apakah berarti mengungu ini berarti sekelas? Tidak juga. Karena jika mengungu kita ubah menjadi relasi lain, misalnya serumah juga akan seperti itu.

Dari sini kita dapat melihat bahwa dalam rangkaian informasi berupa fakta dan aturan yang diberikan oleh Herman, ada sebuah struktur yang dimiliki juga oleh relasi serumah dan sekelas, padahal yang dibicarakan adalah hal-hal yang berbeda.

Ada struktur informasi yang sama antara mengungu, serumah, dan sekelas! Struktur yang sama ini yang kita pelajari secara khusus, terlepas dari apakah makna struktur itu! Melepaskan makna dari struktur dan melihat struktur itu sendiri disebut sebagai proses abstraksi.

Abstraksi

Alih-alih menyebut makhluk-makhluk tersebut dengan nama lengkap, kita dapat menyebut mereka A, E, B, T. Demikian juga kita dapat menuliskan, Amburegul mengungu Emeseyu, sebagai A ∼ E.

Dengan menyingkat kata berarti menjadi simbol ⇒ kita dapat menuliskan kembali hubungan antar krucing sebelumnya (dengan sedikit penyederhanaan) sebagai berikut:

R1
x ∼ x
R2
x ∼ y ⇒ y ∼ x
R3
x ∼ y dan y ∼ z ⇒ x ∼ z
H1
A ∼ B
H2
B ∼ E
H3
B ≁ T
S1
A ∼ A
S2
B ∼ B
S3
E ∼ E
S4
T ∼ E
S5
A ∼ E
S6
E ∼ B
dan seterusnya

Perhatikan bahwa kesimpulan Susi yang pertama, bahwa Amburegul (A) mengungu diri sendiri (A ∼ A), didapat dengan cara menarik kesimpulan sebagai berikut:

R1
x ∼ x
x = A
S1
A ∼ A

Amburegul (A) mengungu Emeseyu (E) juga disimpulkan dengan cara:

R2
x ∼ y dan y ∼ z ⇒ x ∼ z

  (x = A, y = B, z = E)

  A ∼ B dan B ∼ E ⇒ A ∼ E
H1
A ∼ B
H2
B ∼ E
S2
A ∼ E

Mirip seperti matematika, bukan? Apakah ini matematika? Atau apakah masih kurang matematika? Bagaimana jika kita membicarakan hubungan kesamaan antara 4 variabel?

Kasus pembanding: Kesamaan 4 variabel

Terdapat variabel a, e, b, dan t.

A1
a = e
A2
b = e
A3
b ≠ t
R1
x = x
R2
x = y ⇒ y = x
R3
x = y dan y = z ⇒ x = z

Dengan cara yang sama persis seperti sebelumnya, kamu dapat menarik kesimpulan-kesimpulan yang sama.

T1
a = a
T2
b = b
T3
e = e
T4
t = t
T5
a = e
T6
e = b
dan seterusnya

Ini adalah sifat aljabar biasa ketika kita membicarakan kesamaan antar variabel. Yang ini tentu saja adalah matematika. Namun apa yang membedakan dengan hal-hal yang sebelumnya kita bicarakan?

Kenyataannya, sistem pengetahuan semacam ini termasuk dalam pembicaraan matematika yang disebut sebagai relasi biner, yang dinyatakan sebagai sebuah sistem aksiomatik (mengenai ini akan ada bab khusus yang membahasnya).

Relasi Ekivalensi

Masing-masing aturan yang dimiliki relasi mengungu antar krucing memiliki nama.

x ∼ x

R1 disebut sebagai aturan relasi refleksif. Aturan ini mengharuskan setiap objek yang dibicarakan memiliki relasi dengan diri sendiri. Dalam hal krucing, setiap krucing pasti mengungu dirinya sendiri.

x ∼ y ⇒ y ∼ x

R2 disebut sebagai aturan relasi simetrik. Sesuai namanya, aturan ini mengharuskan ada hubungan timbal balik ketika salah satu objek terhubung dengan yang lain.

x ∼ y dan y ∼ z ⇒ x ∼ z

R3 disebut sebagai aturan transitif. Transitif dapat diartikan sebagai menjalar.

Relasi yang mengandung ketiga aturan tersebut (refleksif, simetrik, dan transitif) disebut sebagai relasi ekivalensi.

Beberapa contoh relasi ekivalensi yang dapat kita jumpai sehari-hari misalnya, serumah, sekelas, searah, seumur, sama dengan, dan sebagainya.

Seperti permasalahan jembatan Konigsberg sebelumnya, abstraksi semacam ini memungkinkan kita untuk membicarakan hal yang berbeda dengan cara yang sama.

Jadi sebenarnya matematika itu apa sih?

Berikutnya: Tata Bahasa Mini-Indonesia